【题目】已知抛物线![]() 的顶点为(1,0),且经过点(0,1).
的顶点为(1,0),且经过点(0,1).
(1)求该抛物线对应的函数的解析式;
(2)将该抛物线向下平移m(m>0)个单位,设得到的抛物线的顶点为A,与x轴的两个交点为B、C,若△ABC为等边三角形.
①求m的值;
②设点A关于x轴的对称点为点D,在抛物线上是否存在点P,使四边形CBDP为菱形?若存在,写出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ; (2)①m=3;②不存在这样的点P,理由见解析.
; (2)①m=3;②不存在这样的点P,理由见解析.
【解析】试题分析:(1)根据抛物线的顶点坐标及函数经过点(0,1),利用待定系数法求解即可.
(2)①先写出平移后的函数解析式,然后得出A、B、C三点的坐标,过点A作AH⊥BC于H,根据△ABC为等边三角形,可得出关于m的方程,解出即可;
②求出点D坐标,分两种情况进行讨论,①PD为对角线,②PD为边,根据菱形的性质求解即可.
试题解析:
(1)由题意可得,  解得
解得
∴抛物线对应的函数的解析式为![]() .
.
(2)①将![]() 向下平移m个单位得:
向下平移m个单位得: ![]() -m=
-m= ![]() ,可知A(1,-m),B(1-
,可知A(1,-m),B(1-![]() ,0),C(1+
,0),C(1+![]() ,0),BC=2
,0),BC=2![]() .
.
由△ABC为等边三角形,得![]() ,由m>0,解得m=3.
,由m>0,解得m=3.
②不存在这样的点P.
∵点D与点A关于x轴对称,∴D(1,3).
由①得BC=2![]() .
.
要使四边形CBDP为菱形,需DP∥BC,DP=BC.
由题意,知点P的横坐标为1+2![]() ,
,
当x=1+2![]() 时,
时,
![]() -m=
-m=![]() =
=![]() ,
,
故不存在这样的点P.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l1∥l2∥l3 , 且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图放置,顶点A、B、C恰好分别落在三条直线上,则△ABC的面积为( )

A.
B.
C.12
D.25 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式一定成立的是( )
A. a2+a3=a5 B. (a+b)2=a2+b2
C. (2ab2)3=6a3b6 D. (x-a)(x-b)=x2-(a+b)x+ab
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,王刚在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.2m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触,此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过计算说明.(参考数据:
 ≈1.7)
≈1.7)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则下面结论错误的是( )
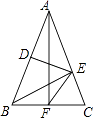
A.BF=EF
B.DE=EF
C.∠EFC=45°
D.∠BEF=∠CBE -
科目: 来源: 题型:
查看答案和解析>>【题目】已知P(5,5),点B、A分别在x的正半轴和y的正半轴上,∠APB=90°,则OA+OB=

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,以下结论:①∠BAC=70°;②∠DOC=90°;③∠BDC=35°;④∠DAC=55°,其中正确的是 . (填写序号)

相关试题

