【题目】如图,A,B,C是⊙O上的三上点,且四边形OABC是菱形,请用无刻度直尺完成下列作图。
(1)如图①,作出线段OA的垂直平分线;
(2)如图②,作出线段BC的垂直平分线。


图① 图②
参考答案:
【答案】见解析
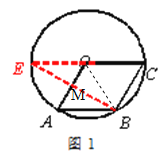
【解析】(1)延长CO交⊙O于点E,连接BE交OA于M.由OABC是菱形的性质得到OC∥AB,OC=AB,通过证明△EOM≌BAM,得到AM=OM.连接OB,得到△OAB是等边三角形,即可得到结论;
(2)在图(1)的基础上,连接AC,交OB于N,作直线MN交BC于F,作直线OF.
由OABC是菱形,得到ON=BN,从而得到MN∥AB,由平行线等分线段定理得到CF=BF,再由等腰三角形的性质即可得出结论.
(1)延长CO交⊙O于点E,连接BE交OA于M.
∵OABC是菱形,∴OC∥AB,OC=AB.
∵EO=OC,∴EO=AB.
∵OC∥AB,∴∠E=∠MBA,∠EOM=∠BAM,∴△EOM≌BAM,∴AM=OM.连接OB,则OB=OA=AB,∴△OAB是等边三角形,∴BM⊥OA,∴BE是OA的垂直平分线.
(2)在图(1)的基础上,连接AC,交OB于N,作直线MN交BC于F,作直线OF.
∵OABC是菱形,∴ON=BN.
∵OM=AM,∴MN∥AB,∴CF=BF.
∵OC=OB,∴OF⊥BC,∴OF为BC的垂直平分线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据a、b、c、d. e方差为3,则另一组数据a+3,b+3,c+3,d+3,e+3的方差为___ ,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=
 ,AD=2,点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F,当BE的长为________时,△CDF为等腰三角形。
,AD=2,点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F,当BE的长为________时,△CDF为等腰三角形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】微信“抢红包”游戏现在受到越来越多的人喜欢,其中有一种玩法“拼手气红包”,用户设置好总金额以及红包个数后,可以随机生成金额不等的红包,现有一用户发了三个“拼手气红包”,总金额为5元,随机被甲、乙、丙三人抢到。
(1)下列事件中,确定事件是__________。
①甲、乙两人抢到的红包金额之和比丙抢到的红包金额多;
②甲抢到的金额为0.5元的红包;
③乙抢到金额为6元的红包。
(2)随机红包分为大、中、小三个金额,用画树状图或列表的方法求出连抽两次最大金额的红包概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市开展“美丽自宫,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在郴州市的日常工作中,洒水车每天都在国庆路上来回洒水.我们约定洒水车在行驶过程中,向北的行程记为正数,向南的行程记为负数.2017年8月20日这一天,某台洒水车市政工程处出发,所走的路程(单位:千米)为:+5,+7.5,-8,-3,+9.5,+2.5,-11,-3.5.问:
(1)这天收工时,这台洒水车离市政工程处多远?它在市政工程处的南边还是北边?
(2)若洒水车每走1千米耗油0.2升,请问这一天这台洒水车在洒水过程中耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:斜率表示一条直线y=kx+b(k≠0)关于橫坐标轴倾斜程度的量,即直线与x轴正方向夹角(倾斜角α)的正切值,表示成k=tanα。
(1)直线y=x-2b的倾斜角α=________。
(2)如图,在△ABC中,tanA、tanB是方程x2-(
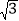 +1)x+
+1)x+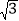 =0的两根,且∠A>∠B,B点坐标为(5,0),求出直线AC关系式。
=0的两根,且∠A>∠B,B点坐标为(5,0),求出直线AC关系式。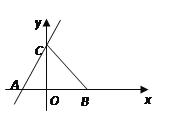
相关试题

