【题目】如图,已知OB是∠AOC的角平分线,OD是∠COE的角平分线,
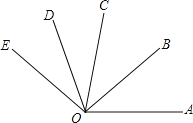
(1)若∠BOE=110°,∠AOB=30°,求∠COE的度数;
(2)若∠AOE=140°,∠AOC=60°,求∠DOE的度数.
参考答案:
【答案】(1)80°;(2)40°.
【解析】
试题分析:(1)由角平分线的定义可知∠BOC=∠AOB,又∠COE=∠BOE﹣∠BOC,易得结果;
(2)由已知易得∠EOC的度数,再利用角平分线的定义可得∠DOE=![]() ,可得结果.
,可得结果.
解:(1)∵∠AOB=30°,OB是∠AOC的角平分线,∠BOE=110°,
∴∠BOC=∠AOB=30°,
∴∠COE=∠BOE﹣∠BOC=110°﹣30°=80°;
(2)∵∠AOE=140°,∠AOC=60°,
∴∠EOC=∠AOE﹣∠AOC=140°﹣60°=80°,
∵OD是∠COE的角平分线,
∴∠DOE=![]() =40°.
=40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△CDE中,已知AC=CD,AC⊥CD,∠B=∠E=90°,则下列结论不正确的是( )
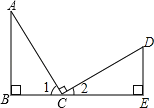
A.∠A与∠D互为余角
B.∠A=∠2
C.△ABC≌△CED
D.∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,点D是BC边上的中点,点E在AD上,那么下列结论不一定正确的是( )
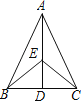
A.AD⊥BC B.∠EBC=∠ECB C.∠ABE=∠ACE D.AE=BE
-
科目: 来源: 题型:
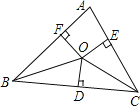
查看答案和解析>>【题目】如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=70°,∠BOC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明用自制的直角三角形纸板DEF测量树AB的高度,他调整自己的位置,使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m, CD=10 m,请你帮小明求下树的高度。
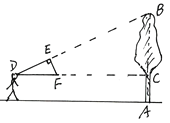
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.

(1)如果随机翻1张牌,那么抽中20元奖品的概率为
(2)如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总值不低于30元的概率为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=
 x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣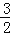 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.
相关试题

