搜索
【题目】如图，大海中某灯塔P周围10海里范围内有暗礁，一艘海轮在点A处观察灯塔P在北偏东60°方向，该海轮向正东方向航行8海里到达点B处，这时观察灯塔P恰好在北偏东45°方向．如果海轮继续向正东方向航行，会有触礁的危险吗？试说明理由．（参考数据：
≈1.73）
参考答案：
【答案】没有触礁的危险．
【解析】
试题分析：作PC⊥AB于C，如图，∠PAC=30°，∠PBC=45°，AB=8，设PC=x，先判断△PBC为等腰直角三角形得到BC=PC=x，再在Rt△PAC中利用正切的定义列方程，求出x的值，即得到AC的值，然后比较AC与10的大小即可判断海轮继续向正东方向航行，是否有触礁的危险．
试题解析：没有触礁的危险．理由如下：
作PC⊥AB于C，如图，∠PAC=30°，∠PBC=45°，AB=8，设PC=x，在Rt△PBC中，∵∠PBC=45°，∴△PBC为等腰直角三角形，∴BC=PC=x，在Rt△PAC中，∵tan∠PAC=
，∴AC=
，即8+x=
，解得x=
≈10.92，即AC≈10.92，∵10.92＞10，∴海轮继续向正东方向航行，没有触礁的危险．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某班举办元旦联欢会，班长对全班同学最爱吃哪几种水果这一问题作出了调查，班长在确定购买哪一种水果时，最值得关注的统计量是（ ）
A.中位数B.平均数C.众数D.加权平均数
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知正方形的边长为a,若边长增加x,则面积增加（ ）
A. (a+x)2 -a2 B. (a-x)2+a2 C. (a+x)2+x2 D. (a-x)2 -x2
-
科目： 来源： 题型：
查看答案和解析>>【题目】现代互联网技术的广泛应用，催生了快递行业的高速发展．小明计划给朋友快递一部分物品，经了解有甲、乙两家快递公司比较合适．甲公司表示：快递物品不超过1千克的，按每千克22元收费；超过1千克，超过的部分按每千克15元收费．乙公司表示：按每千克16元收费，另加包装费3元．设小明快递物品x千克．
（1）请分别写出甲、乙两家快递公司快递该物品的费用y（元）与x（千克）之间的函数关系式；
（2）小明选择哪家快递公司更省钱？
-
科目： 来源： 题型：
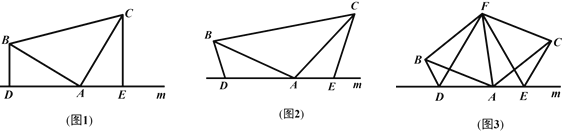
查看答案和解析>>【题目】（1）如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．证明：DE＝BD+CE．
（2）如图2，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？若成立，请给出证明；若不成立，请说明理由．
（3）拓展与应用：如图3，D、E是D、A、E三点所在直线m上的两动点（D、A、E三点
互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA＝∠AEC＝∠BAC，试判断△DEF的形状．
-
科目： 来源： 题型：
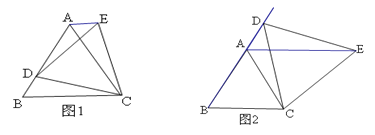
查看答案和解析>>【题目】（1）如图1，D是等边三角形△ABC边BA上任意一点（D与A、B不重合），连接DC，以DC为边在BC边上方作等边三角形△DCE，连接AE，∠ABC与∠EAC有怎样数量关系直接写出结论
（2）如图2，D是等边三角形△ABC边BA延长线上一点，连接DC，以DC为边在BC边上方作等边三角形△DCE，连接AE，求证：∠ABC=∠EAC.
-
科目： 来源： 题型：
查看答案和解析>>【题目】若一元二次方程x2－2x－m＝0无实数根，则一次函数y＝(m＋1)x＋m－1的图象不经过第( )象限．
A. 四 B. 三 C. 二 D. 一
相关试题
