【题目】已知关于x的一元二次方程![]() +ax+a﹣2=0.
+ax+a﹣2=0.
(1)求证:不论a为何实数,此方程总有两个不相等的实数根.
(2)若该方程的两个实数根分别为![]() ,
,![]() ,且
,且![]() =
=![]() ,求a的值.
,求a的值.
参考答案:
【答案】(1)证明详见解析;(2)5或-1.
【解析】
试题分析:(1)根据方程的系数结合根的判别式即可得出△>0,此题得证;
(2)根据根与系数的关系即可得出![]() +
+![]() =﹣a,
=﹣a,![]() ×
×![]() =a﹣2,结合
=a﹣2,结合![]() =
=![]() 即可得出关于a的一元二次方程,解之即可得出a的值.
即可得出关于a的一元二次方程,解之即可得出a的值.
试题解析:(1)在方程![]() +ax+a﹣2=0中,△=
+ax+a﹣2=0中,△=![]() ﹣4(a﹣2)=
﹣4(a﹣2)=![]() +4,
+4,
∵![]() ≥0,
≥0,
∴△>0,
故不论a为何实数,此方程总有两个不相等的实数根;
(2)∵方程![]() +ax+a﹣2=0的两个实数根分别为
+ax+a﹣2=0的两个实数根分别为![]() ,
,![]() ,
,
∴![]() +
+![]() =﹣a,
=﹣a,![]() ×
×![]() =a﹣2,
=a﹣2,
∵![]() =
=![]() ,
,
∴![]() =13,
=13,
∴![]() ,即
,即![]() ﹣4(a﹣2)=13,
﹣4(a﹣2)=13,
整理得:![]() =9,
=9,
解得:![]() =5,
=5,![]() =﹣1,
=﹣1,
所以a的值为5或-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列从左到右的变形,属于因式分解的是( )
A. (x+1)(x-1)=x2-1 B. m2+m-4=(m+3)(m-2)+2 C. x2+2x=x(x+2) D. x2-5x+6=x(x-5) +6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
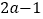 的算术平方根是3,
的算术平方根是3, 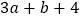 的立方根是2,求
的立方根是2,求 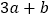 的平方根.
的平方根. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中,其相反数最大的数是( )
A.1B.0C.2D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式中,完全平方式有( )个
a2-4a+4,1+4a2,4b2+4b-1,a2+ab+b2
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=
 ,b=
,b=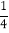 ,c=
,c=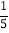 ; ②a=6,b=8,c=10; ③a=7,b=24,c=25;
; ②a=6,b=8,c=10; ③a=7,b=24,c=25;④a=2,b=3,c=4.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种饮料,平均每天可售出100箱,每箱利润为120元,为了扩大销量,尽快减少库存,超市准备适当降价,据测算,若每箱降价2元,则每天可多售出4箱.
(1)如果要使每天销售该饮料获利14000元,则每箱应降价多少元.
(2)每天销售该饮料获利能达到14500元吗?若能,则每箱应降价多少?若不能,请说明理由.
相关试题

