【题目】如图,点D在等边△ABC的边BC上. 
(1)把△ACD绕点A顺时针旋转,使点C与点B重合,画出旋转后的△ABD′;
(2)如果AC=4,CD=1,求(1)中点D旋转所走过的路程.
参考答案:
【答案】
(1)解:)如图,△ABD′即为所求;

(2)解:过点A作AE⊥BC于点E,
∵△ABC是等边三角形,
∴CE= ![]() BC=
BC= ![]() ×4=2,ED=CE﹣CD=2﹣1=1.
×4=2,ED=CE﹣CD=2﹣1=1.
∴在Rt△AEC中,AE= ![]() =
= ![]() =2
=2 ![]() .
.
同理,AD= ![]() =
= ![]() =
= ![]() ,
,
∴点D旋转走过的路程为: ![]() =
= ![]() .
.
【解析】(1)根据图形旋转的性质画出图形即可;(2)过点A作AE⊥BC于点E,根据等边三角形的性质求出CE的长,进而可得出ED的长,根据勾股定理求出AE及AD的长,由扇形的面积公式即可得出结论.
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在1×3的正方形网格格点上放三枚棋子,按图所示的位置己放置了两枚棋子,若第三枚棋子随机放在其他格点上,则以这三枚棋子所在的格点为顶点的三角形是直角三角形的概率为 .
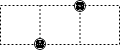
-
科目: 来源: 题型:
查看答案和解析>>【题目】为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1、2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.
(1)求1号线,2号线每千米的平均造价分别是多少亿元?
(2)除1、2号线外,长沙市政府规划到2018年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c (a≠0)(a≠0,a,b,C为常数)的图象,若关于x的一元二次方程ax2+bx+c=m有实数根,则m的取值范围是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】一天,小明和小智一起玩卡片游戏,他们分别握有三张正面分别标有字母A,B,C,的不透明卡片.游戏约定:每人将各自的卡片背面朝工弄洗均匀,然后随机抽取一张,两张卡片中,如果同为元音或辅音字母,则为平局;如果一个元音字母一个辅音字母,则抽到元音字母者获胜.
(1)请用列表或画树状图的方法列举出所有出现结果的可能性;
(2)求小明获胜的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年9月5日,二十国集团领导人杭州峰会在杭州国际博览中心继续举行,这次峰会吸引了大批游客在“十一”假期间前往杭州旅游.为抓住商机,两个商家对同样一件售价为50元/个的产品进行促销活动.甲商家用如下方法促销:若购买该商品不超过l0个,按原价付款:若一次购买l0个以上.且购买的个数每增加一个,其价格减少l元,但该商品的售价不得低于35元/个;乙店一律按原价的80%销售.现购买该商品x个,如果全部在甲商家购买,则所需金额为y1元:如果全部在乙商家购买,则所需金额为y2元.
(1)分别求出yl , y2与x之间的函数关系式;
(2)若一位游客花800元,最多能购买多少个该商品? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
(1)如图①,当直线l与⊙O相切于点C时,求证:AC平分∠DAB;
(2)如图②,当直线l与⊙O相交于点E,F时,求证:∠DAE=∠BAF.
相关试题

