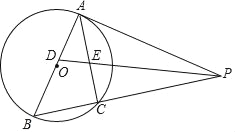
【题目】如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x2﹣5x+6=0的两个实数根.
(1)求证:PABD=PBAE;
(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.
参考答案:
【答案】(1)证明见解析;(2)存在,![]()
【解析】(1)易证∠APE=∠BPD,∠EAP=∠B,从而可知△PAE∽△PBD,利用相似三角形的性质即可求出答案.
(2)过点D作DF⊥PB于点F,作DG⊥AC于点G,易求得AE=2,BD=3,由(1)可知:![]() ,从而可知cos∠BDF=cos∠BAC=cos∠APC=
,从而可知cos∠BDF=cos∠BAC=cos∠APC=![]() ,从而可求出AD和DG的长度,进而证明四边形ADFE是菱形,此时F点即为M点,利用平行四边形的面积即可求出菱形ADFE的面积.
,从而可求出AD和DG的长度,进而证明四边形ADFE是菱形,此时F点即为M点,利用平行四边形的面积即可求出菱形ADFE的面积.
(1)∵PD平分∠APB,
∴∠APE=∠BPD,
∵AP与⊙O相切,
∴∠BAP=∠BAC+∠EAP=90°,
∵AB是⊙O的直径,
∴∠ACB=∠BAC+∠B=90°,
∴∠EAP=∠B,
∴△PAE∽△PBD,
∴![]() ,
,
∴PABD=PBAE;
(2)如图,过点D作DF⊥PB于点F,作DG⊥AC于点G,
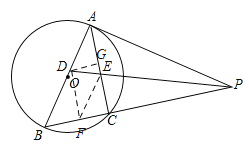
∵PD平分∠APB,AD⊥AP,DF⊥PB,
∴AD=DF,
∵∠EAP=∠B,
∴∠APC=∠BAC,
易证:DF∥AC,
∴∠BDF=∠BAC,
由于AE,BD(AE<BD)的长是x2﹣5x+6=0的两个实数根,
解得:AE=2,BD=3,
∴由(1)可知:![]() ,
,
∴cos∠APC=![]() ,
,
∴cos∠BDF=cos∠APC=![]() ,
,
∴![]() ,
,
∴DF=2,
∴DF=AE,
∴四边形ADFE是平行四边形,
∵AD=DF,
∴四边形ADFE是菱形,此时点F即为M点,
∵cos∠BAC=cos∠APC=![]() ,
,
∴sin∠BAC=![]() ,
,
∴![]() ,
,
∴DG=![]() ,
,
∴菱形ADME的面积为:DGAE=2×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“推进全科阅读,培育时代新人”.某学校为了更好地开展学生读书活动,随机调查了八年级50名学生最近一周的读书时间,统计数据如下表:
时间(小时)
6
7
8
9
10
人数
5
8
12
15
10
(1)写出这50名学生读书时间的众数、中位数、平均数;
(2)根据上述表格补全下面的条形统计图.
(3)学校欲从这50名学生中,随机抽取1名学生参加上级部门组织的读书活动,其中被抽到学生的读书时间不少于9小时的概率是多少?
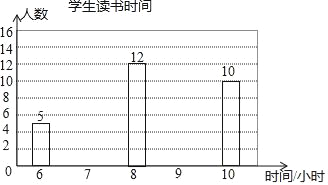
-
科目: 来源: 题型:
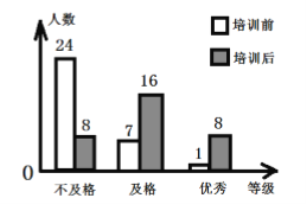
查看答案和解析>>【题目】某校八年级320名学生在电脑培训前后各参加了一次水平相同的考试,考试成绩都以统一标准划分成“不及格”“及格”和“优秀”三个等级.为了解电脑培训的效果,用抽签方式得到其中32名学生培训前后两次成绩的等级,并绘制成如图所示的统计图,请结合图中信息估计该校整个八年级学生中,培训后考试成绩的等级为“及格”和“优秀”的学生共有______名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y1=﹣x+4,y2=
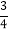 x+b都与双曲线y=
x+b都与双曲线y= 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式
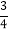 x+b>
x+b> 的解集;
的解集;(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个底面直径为5cm,高为16cm圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃杯中,能否完全装下?若装不下,求瓶内水面还有多高?若未能装满,求玻璃杯内水面离杯口的距离?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)操作发现:如图①,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是__________;位置关系是__________.
(2)类比思考:
如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其它条件不变,小明发现的上述结论还成立吗?请说明理由.
(3)深入研究:
如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其它条件不变,试判断△GMN的形状,并给与证明.

相关试题

