【题目】已知:如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O .

(1)求证:AB=DC;
(2)求证:△OEF是等腰三角形.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析: (1)根据BE=CF得到BF=CE,又∠A=∠D,∠B=∠C,所以△ABF≌△DCE,根据全等三角形对应边相等即可得证;
(2)根据三角形全等得∠AFB=∠DEC,所以是等腰三角形.
试题解析:
(1)∵BE=CF ,
∴BF= CE ,
∵在△ABF和△DCE中,
 ,
,
∴△ABF≌△DCE(AAS) ,
∴AB=DC ;
(2)∵△ABF≌△DCE ,
∴∠AFB=∠DEC ,
∴OE=OF ,
∴△OEF是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A=2a2+3ab﹣2a﹣1,B=﹣a2+ab﹣1.
(1)求3A+6B;
(2)若3A+6B的值与a的取值无关,求b的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师在黑板上出了一道解方程的题:4(2x﹣1)=1﹣3(x+2),小明马上举手,要求到黑板上做,他是这样做的:8x﹣4=1﹣3x+6,①
8x﹣3x=1+6﹣4,②
5x=3,③
x=
 .④
.④老师说:小明解一元一次方程没有掌握好,因此解题时出现了错误,请你指出他错在哪一步:________(填编号),并说明理由.然后,你自己细心地解这个方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x3﹣4x2+4x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解宿迁市中小学生对中华古诗词喜爱的程度,这项调查采用_____方式调查较好(填“普查”或“抽样调查”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图.
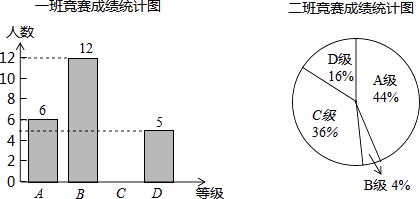
平均数(分)
中位数(分)
众数(分)
一班
a
b
90
二班
d
80
c
(1)把一班竞赛成绩统计图补充完整;
(2)写出表中a、b、c的值:平均数(分)
中位数(分)
众数(分)
一班
a
b
90
二班
d
80
c
(3)请从平均数和中位数方面比较一班和二班的成绩,对这次竞赛成绩的结果进行分析. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.随机抛掷一枚硬币,反面一定朝上
B.数据3,3,5,5,8的众数是8
C.某商场抽奖活动获奖的概率为 ,说明毎买50张奖券中一定有一张中奖
,说明毎买50张奖券中一定有一张中奖
D.想要了解广安市民对“全面二孩”政策的看法,宜采用抽样调查
相关试题

