【题目】如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,连接OH. 
(1)求AD与DH的长;
(2)求证:∠HDO=∠DCO.
参考答案:
【答案】
(1)解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC= ![]() AC=4cm,OB=OD=3cm,
AC=4cm,OB=OD=3cm,
∴AB=AD=5cm,
∴S菱形ABCD= ![]() ACBD=ABDH,
ACBD=ABDH,
∴DH= ![]() =4.8(cm)
=4.8(cm)
(2)证明:∵AB∥CD,
∴∠ABD=∠CDB,
∵∠ABD+∠HDO=90°,∠CDB+∠DCO=90°,
∴∠HDO=∠DCO.
【解析】(1)根据菱形的面积等于对角线积的一半,可求得菱形的面积,又由菱形的对角线互相平分且垂直,可根据勾股定理得AB的长,根据菱形的面积的求解方法:底乘以高或对角线积的一半,即可得菱形的高;(2)直接利用平行线的性质得出∠ABD=∠CDB,进而利用互余的性质得出答案.
【考点精析】认真审题,首先需要了解菱形的性质(菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半).
-
科目: 来源: 题型:
查看答案和解析>>【题目】请将下列事件发生的概率标在图中.
(1)抛出的篮球会下落;
(2)从装有3个红球、7个白球的口袋中取一个球,恰好是红球(这些球除颜色外完全相同);
(3)掷一枚质地均匀的硬币,硬币落下后正面朝上.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣6x图象的顶点坐标为( )
A.(3,0)B.(﹣3,﹣9)C.(3,﹣9)D.(0,﹣6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】能把一个三角形分成两个面积相等的三角形的是( )
A. 角平分线B. 高C. 中线D. 一边的垂直平分线
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列长度的三条线段为边,不能组成直角三角形的是( )
A. 1、1、2 B. 6、8、10 C. 5、12、13 D. 3、4、5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x﹣2y=3,那么代数式3﹣2x+4y的值是( )
A.﹣3
B.3
C.6
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,点M、N在直线BD上,点M在N点左侧,AM∥CN.

(1)如图1,求证:BM=DN;
(2)如图2,当∠ABC=90°,点M,N在线段BD上时,求证:BM+BN=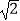 AB;
AB;
(3)如图3,当∠ABC=60°,点M在线段DB的延长线上时,直接写出BM,BN,AB三者的数量关系.
相关试题

