搜索
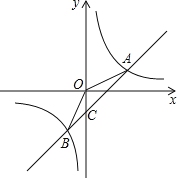
【题目】如图，已知反比例函数的图象
与一次函数
的图象交于
两点，且
．
(1)求反比例函数和一次函数的关系式；
(2)利用图象直接写出当
在什么范围时， 
；
（3）求出三角形AOB的面积.
参考答案：
【答案】（1）
（2）
或
（3）
【解析】试题分析：（1）将点A（2，n），B（﹣1，﹣2）代入反比例函数y1=
中得：2n=（﹣1）×（﹣2）=k1，可求k1、n；再将点A（2，n），B（﹣1，﹣2）代入y2=k2x+b中，列方程组求k2、b即可；
（2）根据两函数图象的交点，图象的位置可确定y1＞y2时x的范围；
（3）要求△AOB的面积，可以分两部分求解．首先根据直线AB的解析式求得与y轴的交点坐标，进一步根据y轴所分成的两个三角形的面积求解．
试题解析：解：（1）∵双曲线y1=
过点（﹣1，﹣2），∴k1=﹣1×（﹣2）=2．
∵双曲线y1=
，过点（2，n），∴n=1．
由直线y2=k2x+b过点A，B得：
，解得
，∴反比例函数关系式为y1=
，一次函数关系式为y2=x﹣1．
（2）根据图象得出：当x＜﹣1或0＜x＜2时，y1＞y2．
（3）由一次函数的解析式，得直线AB与y轴的交点是（0，﹣1），则△AOB的面积=S△BCO+S△ACO=
×1×1+
×1×2=
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如表（单位：环）：
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
（1）根据表格中的数据，分别计算甲、乙的平均成绩；
（2）已知甲六次成绩的方差S甲2=
，试计算乙六次测试成绩的方差；根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】学生的学业负担过重会严重影响学生对待学习的态度．为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查（把学习态度分为三个层级，A级：对学习很感兴趣；B级：对学习较感兴趣；C级：对学习不感兴趣），并将调查结果绘制成图①和图②的统计图（不完整）．请根据图中提供的信息，解答下列问题：
（1）此次抽样调查中，共调查了 名学生；
（2）将图①补充完整；
（3）求出图②中C级所占的圆心角的度数；
（4）根据抽样调查结果，请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标（达标包括A级和B级）？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一个暗箱中装有红、黄、白三种颜色的乒乓球（除颜色外其余均相同）．其中白球、黄球各1个，若从中任意摸出一个球是白球的概率是
．
（1）求暗箱中红球的个数．
（2）先从暗箱中任意摸出一个球记下颜色后放回，再从暗箱中任意摸出一个球，求两次摸到的球颜色不同的概率（用树形图或列表法求解）． -
科目： 来源： 题型：
查看答案和解析>>【题目】国家规定，中小学生每天在校体育活动时间不低于1小时，为了解这项政策的落实情况，有关部门就“你某天在校体育活动时间是多少”的问题，在某校随机抽查了部分学生，再根据活动时间t（小时）进行分组（A组：t＜0.5，B组：0.5≤t＜1，C组：1≤t＜1.5，D组：t≥1.5），绘制成如下两幅不完整统计图，请根据图中信息回答问题：
（1）此次抽查的学生数为人，并补全条形统计图；
（2）从抽查的学生中随机询问一名学生，该生当天在校体育活动时间低于1小时的概率是；
（3）若当天在校学生数为1200人，请估计在当天达到国家规定体育活动时间的学生有人． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图①已知正方形ABCD的边BC、CD上分别有E、F两点，且∠EAF=45°，现将△ADF绕点A顺时针旋转90°至△ABH处.
（1）线段EF、BE、DF有何数量关系？并说明理由；
模仿（1）中的方法解决（2）、（3）两个问题：
（2）如图②，若将E、F移至BD上，其余条件不变，且BE=
，DF=3，求EF的长；（3）如图③，图形变成矩形ABCD，∠EAF=45°，BE=3，AB=6，AD=10，求DF和EF的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的边长为5，点A的坐标为（﹣4，0），点B在y轴上，若反比例函数
（k≠0）的图象过点C，则该反比例函数的表达式为（ ）
A.
B. 
C. 
D. 
相关试题
