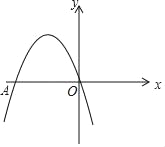
【题目】如图,二次函数y=ax2﹣4x+c的图象经过坐标原点,与x轴交于点A(﹣4,0)
(1)求此二次函数的解析式,并求出抛物线的顶点坐标;
(2)在抛物线上存在点P,使△AOP的面积为10?求出点P的坐标.
参考答案:
【答案】(1)y=﹣x2﹣4x;(2)P坐标为(﹣5,﹣5),(1,﹣5).
【解析】(1)把原点与A坐标代入解析式求出a与c的值,即可确定出解析式;
(2)由A与O坐标求出AO的长,根据三角形AOP面积为10,利用面积公式求出P纵坐标的绝对值为5,即P纵坐标为5或-5,把y=5或y=-5代入抛物线解析式求出x的值,即可确定出P坐标.
解:(1)把(0,0)与(﹣4,0)代入得:![]() ,
,
解得:a=﹣1,c=0,
则抛物线解析式为y=﹣x2﹣4x;
(2)∵AO=4,S△AOP=10,
∴|yP纵坐标|=5,即yP纵坐标=5或yP纵坐标=﹣5,
把y=5代入抛物线解析式得:x2+4x+5=0,方程无解;
把y=﹣5代入抛物线解析式得:x2+4x﹣5=0,解得x=﹣5或x=1,
此时P坐标为(﹣5,﹣5),(1,﹣5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小马虎解方理
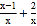 =3出现了错误,解答过程如下:
=3出现了错误,解答过程如下:方程两边都乘以x,得x﹣1+2=3(第一步)
移项,合并同类项,得x=2(第二步)
经检验,x=2是原方程的解(第三步)
(1)小马虎解答过程是从第 步开始出错的,出错原因是 ;
(2)请写出此题正确的解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据:
 ≈1.4,
≈1.4,  ≈1.7).
≈1.7).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为准备参加某市2019年度中小学生机器人竞赛,学校对甲、乙两支机器人制作小队所创作的机器人分别从创意、设计、编程与制作三方面进行量化,各项量化满分100分,根据量化结果择优推荐.它们三项量化得分如下表:
量化项目
量化得分
甲队
乙队
创意
85
72
设计
70
66
编程与制作
64
84
(1)如果根据三项量化的平均分择优推荐,哪队将被推荐参赛?
(2)根据本次中小学生机器人竞赛的主题要求,如果学校根据创意、设计、编程与制作三项量化得分按
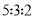 的比例确定每队最后得分的平均分择优推荐,哪队将被推荐参赛?并对另外一队提出合理化的建议.
的比例确定每队最后得分的平均分择优推荐,哪队将被推荐参赛?并对另外一队提出合理化的建议. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读某同学对多项式
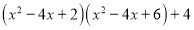 进行因式分解的过程,并解决问题:
进行因式分解的过程,并解决问题:解:设
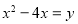 ,
,原式
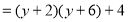 (第一步)
(第一步)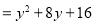 (第二步)
(第二步)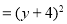 (第三步)
(第三步)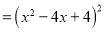 (第四步)
(第四步)(1)该同学第二步到第三步的变形运用了________(填序号);
A.提公因式法 B.平方差公式
C.两数和的平方公式 D.两数差的平方公式
(2)该同学在第三步用所设的的代数式进行了代换,得到第四步的结果,这个结果能否进一步因式分解?________(填“能”或“不能”).如果能,直接写出最后结果________.
(3)请你模仿以上方法尝试对多项式
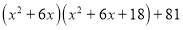 进行因式分行解.
进行因式分行解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为直线AB上一点,过点O作射线OC,使
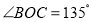 .将一个含
.将一个含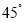 角的直角三角板OMN的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边ON,MN都在直线AB的下方.
角的直角三角板OMN的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边ON,MN都在直线AB的下方.
(1)将图1中的三角板OMN绕着点O逆时针旋转
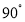 ,如图2所示,请问OM是否平分
,如图2所示,请问OM是否平分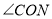 ?请说明理由;
?请说明理由;(2)将图2中的三角板OMN绕点O逆时针继续旋转到图3的位置所示,使得ON在
 的内部,请探究
的内部,请探究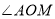 与
与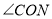 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;(3)将图1中的三角板OMN绕点O按每秒
 的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直角边ON所在直线恰好平分锐角
的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直角边ON所在直线恰好平分锐角 ,则t的值为________(直接写出结果).
,则t的值为________(直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】小明从家到学校上学,沿途需经过三个路口,每个路口都设有红、绿两种颜色的信号灯,在信号灯正常情况下:
(1)请用树状图列举小明遇到交通信号灯的所有情况;
(2)小明遇到两次绿色信号的概率有多大?
(3)小明红绿色两种信号都遇到的概率有多大?
相关试题

