【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3s后,两点相距18个单位长度.已知点B的速度是点A的速度的5倍(速度单位:单位长度/s).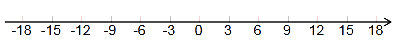
(1)求出点A、点B运动的速度,并在数轴上标出A,B两点从原点出发运动3s时的位置;
(2)若A,B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)当A,B两点从(2)中的位置继续以原来的速度沿数轴向左运动的同时,另一点C从原点位置也向点A运动,当遇到点A后,立即返回向点B运动,遇到点B后又立即返回向点A运动,如此往返,直到点B追上点A时,点C立即停止运动.若点C一直以8个单位长度/s的速度匀速运动,则点C从开始运动到停止运动,行驶的路程是多少个单位长度?
参考答案:
【答案】
(1)解:设点A的速度为每秒t个单位,则点B的速度为每秒5t个单位,由题意,得:
3t+3×5t=18,
解得:t=1,
∴点A的速度为每秒1个单位长度,则点B的速度为每秒5个单位长度.
如图:![]()
(2)解:设x秒时原点恰好在A、B的中间,由题意,得
3+x=15-5x,
解得:x=2.
∴2秒时,原点恰好处在点A、点B的正中间
(3)解:由题意,得
B追上A的时间为:10÷(5-1)=2.5秒,
∴C行驶的路程为:2.5×10=25个单位长度
【解析】(1)根据图形找出各条线段之间的关系量,列出一元一次方程,求出点A的速度为每秒1个单位长度,则点B的速度为每秒5个单位长度;(2)根据题意和中点的定义,找出相等的关系量,列出一元一次方程,求出原点恰好处在点A、点B的正中间的时间;(3)根据题意得到B追上A的时间为10÷(5-1),C行驶的路程为2.5×10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
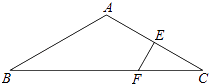
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(﹣2,3)关于原点O对称的点B(b,c),则b+c= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣x2+4x﹣1的顶点坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】用棋子摆出下列一组三角形,三角形每边有n枚棋子,每个三角形的棋子总数为s,如图按此规律推断,当三角形的边上有n枚棋子时,该三角形棋子总数s=(用含n的式子表示).
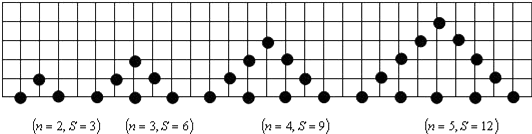
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.
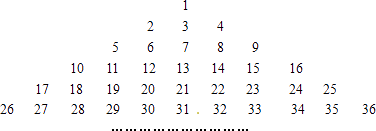
(1)表中第8行的最后一个数是 , 它是自然数的平方,第8行共有个数;
(2)用含n的代数式表示:第n行的第一个数是 , 最后一个数是 , 第n行共有个数;
(3)求第n行各数之和. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列选项中.与xy2是同类项的是( )
A.﹣2xy2
B.2x2y
C.xy
D.x2y2
相关试题

