【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,
(1)求∠BPQ的度数.
(2)求证:BP=2PQ.

参考答案:
【答案】见解析
【解析】试题分析:
(1)由△ABC是等边三角形可得:AB=AC,∠BAE=∠ACD=60°,结合已知AE=CD,易证△BAE≌△ACD,从而可得∠ABE=∠CAD;由三角形外角的性质易得:∠BPQ=∠BAP+∠ABE,再由∠BAP+∠CAE=∠BAC=60°,可得∠BPQ=∠BAP+∠ABE=∠BAP+∠CAE=60°;
(2)由BQ⊥AD于Q可得∠BQP=90°,结合∠BPQ=60°可得∠PBQ=30°,由直角三角形中30°的锐角所对直角边是斜边的一半可得:PQ=![]() BP,∴BP=2PQ.
BP,∴BP=2PQ.
试题解析:
(1)∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,
∵AB=AC,∠BAE=∠C=60°,AE=CD,
∴△ABE≌△CAD(SAS),
∴∠ABE=∠CAD,
∴∠BPQ=∠BAP+∠ABE=∠BAP+∠CAD=60°.
(2)∵BQ⊥AD,
∴∠BQP=90°,
∴∠PBQ=90°﹣∠BPQ=90°﹣60°=30°,
∴BP=2PQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
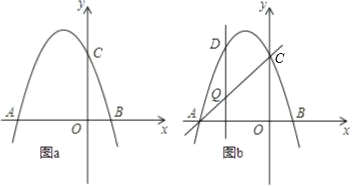
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果钟面上的时间是8:30,则分针与时针的夹角是_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+ax+a﹣2=0
(1)若该方程的一个根为1,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式,并将解集在数轴上表示出来:
 ﹣
﹣ >﹣2.
>﹣2. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某校“我的中国梦”演讲比赛中,有9名学生参加比赛,他们决赛的最终成绩各不相同,其中的一名学生要想知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )
A. 众数 B. 方差 C. 平均数 D. 中位数
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.m2+m2=m4B.(m2)3=m5C.m+2=2mD.(mn)3=m3n3
相关试题

