【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,AG交CD于K,E为CD延长线上一点,且EK=EG,EG的延长线交AB的延长线于F. 
(1)求证:EF为⊙O的切线;
(2)若DK=2HK=AK,CH= ![]() ,求图中阴影部分的面积S.
,求图中阴影部分的面积S.
参考答案:
【答案】
(1)证明:连接OG,如图1所示:

∵弦CD⊥AB于点H,
∴∠AHK=90°,
∴∠HKA+∠KAH=90°,
∵EG=EK,
∴∠EGK=∠EKG,
∵∠HKA=∠GKE,
∴∠HAK+∠KGE=90°,
∵AO=GO,
∴∠OAG=∠OGA,
∴∠OGA+∠KGE=90°,
∴GO⊥EF,
∴EF是⊙O的切线
(2)解:∵CD⊥AB,
∴DH=CH= ![]() ,
,
∵DK=2HK=AK,
∴∠HAK=30°,HK= ![]() DH=
DH= ![]() ,
,
∴AH= ![]() HK=
HK= ![]() ,
,
连接OD,如图2所示:

设⊙O的半径为R,
在Rt△ODH中,由勾股定理得:( ![]() )2+(R﹣
)2+(R﹣ ![]() )2=R2,
)2=R2,
解得:R=2 ![]() ,
,
∴OH=OA﹣AH= ![]() =
= ![]() OD,
OD,
∴∠ODH=30°,△ODH的面积= ![]() OHDH=
OHDH= ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
∴∠DOH=60°,
∴∠BOD=120°,
∴扇形OBGD的面积= ![]() =
= ![]() ,
,
∵OA=OG,
∴∠OGA=∠HAK=30°,
∴∠EGK=90°﹣30°=60°,
又∵EK=EG,
∴△GEK是等边三角形,
∴∠E=60°,
∴∠F=90°﹣60°=30°,
∵GO⊥EF,
∴OF=2OG=4 ![]() ,
,
∴HF=OH+OF=5 ![]() ,
,
∴HE= ![]() HF=
HF= ![]()
∴△EFH的面积= ![]() HFHE=
HFHE= ![]() ×5
×5 ![]() ×
× ![]() =
= ![]() ,
,
∴图中阴影部分的面积S= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]()
【解析】(1)连接OG,首先证明∠EGK=∠EKG,再证明∠HAK+∠KGE=90°,进而得到∠OGA+∠KGE=90°即GO⊥EF,进而证明EF是⊙O的切线;(2)与已知条件得出∠HAK=30°,HK= ![]() DH=
DH= ![]() ,AH=
,AH= ![]() HK=
HK= ![]() ,连接OD,设⊙O的半径为R,在Rt△ODH中,由勾股定理得出方程,解方程求出半径,得出OH=
,连接OD,设⊙O的半径为R,在Rt△ODH中,由勾股定理得出方程,解方程求出半径,得出OH= ![]() OD,求出∠ODH=30°,△ODH的面积=
OD,求出∠ODH=30°,△ODH的面积= ![]() ,再求出∠BOD=120°,得出扇形OBGD的面积=
,再求出∠BOD=120°,得出扇形OBGD的面积= ![]() ,证明△GEK是等边三角形,求出OF=2OG=4
,证明△GEK是等边三角形,求出OF=2OG=4 ![]() ,得出HF=OH+OF=5
,得出HF=OH+OF=5 ![]() ,求出HE=
,求出HE= ![]() ,计算出△EFH的面积,即可得出结果.
,计算出△EFH的面积,即可得出结果.
【考点精析】关于本题考查的垂径定理和扇形面积计算公式,需要了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.有以下说法:①小文同学一共统计了60人;②每天微信阅读不足20分钟的人数有8人;③每天微信阅读30~40分钟的人数最多;④每天微信阅读0-10分钟的人数最少.根据图中信息,上述说法中正确的是( )

A. ①②③④ B. ①②③ C. ②③④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校园内有一块菱形的空地ABCD,为了美化环境,现要进行绿化,计划在中间建设一个面积为S的矩形绿地EFGH,其中,点E、F、G、H分别在菱形的四条边上,AB=a米,BE=BF=DG=DH=x米,∠A=60°

(1)求S关于x的函数关系式,并直接写出自变量x的取值范围;
(2)若a=100,求S的最大值,并求出此时x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=kx﹣k与
 在同一坐标系中的大致图象是( )
在同一坐标系中的大致图象是( )
A.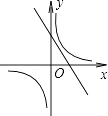
B.
C.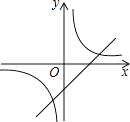
D.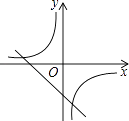
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某次人才交流会上,应聘人数和招聘人数分别居前5位的行业列表如下:


如果用同一行业应聘人数与招聘人数比值的大小来衡量该行业的就业情况,那么根据表中数据,对上述行业的就业情况判断正确的是( )
A. 计算机行业好于其它行业 B. 贸易行业好于化工行业
C. 机械行业好于营销行业 D. 建筑行业好于物流行业
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图。

(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐。据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
相关试题

