Question

【题目】直线AB、CD相交于点O.

(1)OE、OF分别是∠AOC、∠BOD的平分线.画出这个图形.

(2)射线OE、OF在同一条直线上吗?(直接写出结论)

(3)画∠AOD的平分线OG.OE与OG有什么位置关系?并说明理由.

Answer 1

【答案】（1）作图见解析；（2）射线OE、OF在同一条直线上（3）OE⊥OG 理由见解析.

【解析】试题分析：（1）根据题意画图；

（2）根据邻补角和对顶角的定义得到∠AOC=∠BOD，∠AOC+∠AOD=180°，再根据角平分线的定义得∠AOE=∠AOC，∠DOF=∠BOD，则∠AOE=∠DOF，所以∠AOE+∠DOF+∠AOD=180°，于是可判断射线OE、射线OF在同一条直线上；

（3）根据（2）得∠AOE=∠DOF，∠AOE+∠DOF+∠AOD=180°，再由OG平分∠AOD得∠AOG=∠DOG，所以∠AOE+∠AOG=90°．

试题解析：解：（1）如图；

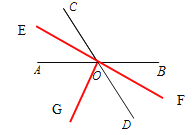
（2）射线OE、射线OF在同一条直线上．理由如下：

∵直线AB、CD相交于点O，∴∠AOC=∠BOD，∠AOC+∠AOD=180°．∵OE、OF分别是∠AOC、∠BOD的平分线，∴∠AOE=∠AOC，∠DOF=∠BOD，∴∠AOE=∠DOF，∴∠AOE+∠DOF=∠AOC，∴∠AOE+∠DOF+∠AOD=180°，∴射线OE、射线OF在同一条直线上；

（3）如图，OE⊥OG．理由如下：

∵OG平分∠AOD，∴∠AOG=∠DOG．∵∠AOE=∠DOF，∠AOE+∠DOF+∠AOD=180°，∴∠AOE+∠AOG=90°，∴OG⊥OE．