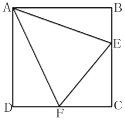
【题目】如图,E与F分别在正方形ABCD边BC与CD上,∠EAF=45°.
(1)以A为旋转中心,将△ABE按顺时针方向旋转90°,画出旋转后得到的图形.
(2)已知BE=2cm,DF=3cm,求EF的长.
参考答案:
【答案】(1)见解析;(2)5cm.
【解析】(1)根据旋转角度、旋转方向、旋转点找出各点的对应点,顺次连接即可得出;
(2)首先证明△ABE≌△ADM,进而得到∠MAF=45°;证明△EAF≌△MAF,得到EF=FG问题即可解决.
(1)如图所示;
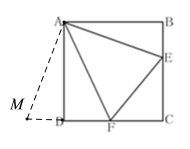
(2)由(1)知:△ADM≌△ABE,M、D、F共线,
∴AD=AB,AM=AE,∠MAD=∠BAE,MD=BE=2,
∵四边形ABCD为正方形,∠EAF=45°,∴∠BAE+∠DAF=45°,
∴∠MAD+∠DAF=45°,
∴△AMF≌△AEF(SAS),
∴EF=MF,
∵MF=MD+DF,
∴EF=MF=MD+DF=2+3=5cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.
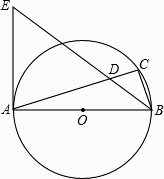
(1)∠ACB=°,理由是:;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形的上底为
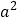 +2
+2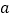 -10,下底为3
-10,下底为3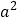 -5
-5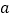 -80,高为40.(
-80,高为40.(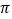 取3)
取3)(1)用式子表示图中阴影部分的面积;
(2)当
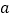 =10时,求阴影部分面积的值。
=10时,求阴影部分面积的值。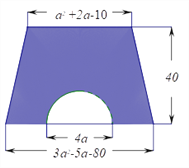
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD//BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
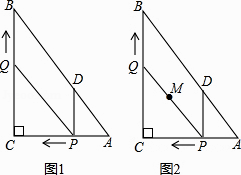
(1)直接用含t的代数式分别表示:QB= , PD= .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
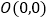 ,
, 是正方形
是正方形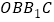 的两个顶点,以它的对角线
的两个顶点,以它的对角线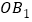 为一边作正方形
为一边作正方形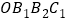 ,以正方形
,以正方形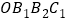 的对角线
的对角线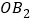 为一边作正方形
为一边作正方形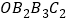 ,再以正方形
,再以正方形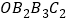 的对角线
的对角线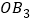 为一边作正方形
为一边作正方形 ,…,依次进行下去,则点
,…,依次进行下去,则点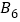 的坐标是( )
的坐标是( )
A.
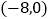 B.
B. 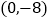 C.
C. 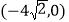 D.
D. 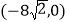
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出如下问题:

小凯的作法如下:
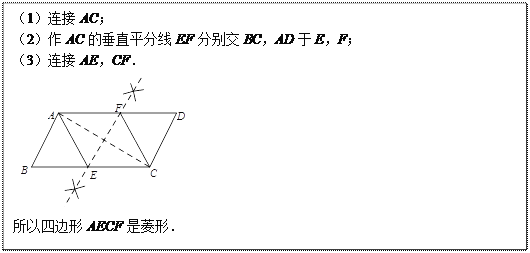
老师说:“小凯的作法正确.”
请回答:在小凯的作法中,判定四边形AECF是菱形的依据是______________________.
相关试题

