【题目】综合题如图1,在边长为a的正方形中
(1)画出两个长方形阴影,则阴影部分的面积是(写成两数平方差的形式);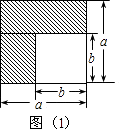
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的长是 , 宽是 , 面积是(写成多项式乘法的形式);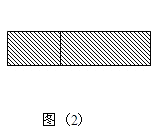
(3)比较左、右两图的阴影部分面积,可以得到乘法公式(用式子表达);
(4)运用你所得到的公式计算:
①10.3×9.7
②(2m+n﹣p)(2m﹣n+p)
参考答案:
【答案】
(1)a2﹣b2
(2)a+b,a﹣b,(a+b)(a﹣b)
(3)a2﹣b2=(a+b)(a﹣b)
(4)解:①10.3×9.7=(10+0.3)(10﹣0.3)=100﹣0.09=99.91;
②(2m+n﹣p)(2m﹣n+p)=[2m+(n﹣p)][2m﹣(n﹣p)]=(2m)2﹣(n﹣p)2=4m2﹣n2+2np﹣p2.
【解析】解:(1)∵大正方形的面积=a2,小正方形的面积=b2,
∴阴影部分的面积为:a2﹣b2,
所以答案是:a2﹣b2;(2)将阴影部分裁剪下来,重新拼成一个长方形,它的长是a+b,宽是a﹣b,面积是(a+b)(a﹣b);
所以答案是:a+b,a﹣b,(a+b)(a﹣b);(3)因而得到乘法公式是a2﹣b2=(a+b)(a﹣b);
所以答案是:a2﹣b2=(a+b)(a﹣b);
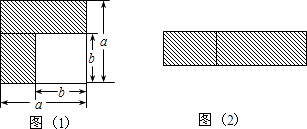
(1)第一个图形中阴影部分的面积计算方法是边长是a的正方形的面积减去边长是b的小正方形的面积,等于a2-b2;
(2)第二个图形阴影部分是一个长是(a+b),宽是(a-b)的长方形,面积是(a+b)(a-b);
(3)根据这两个图形的阴影部分的面积相等即可得到结论;
(4)根据平方差公式即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AD平分∠CAE,AD∥BC.
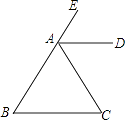
(1)求证:△ABC是等腰三角形.
(2)当∠CAE等于多少度时△ABC是等边三角形?证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点M(﹣2,3)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】(﹣0.7)2的平方根是( )
A.﹣0.7
B.0.7
C.±0.7
D.0.49 -
科目: 来源: 题型:
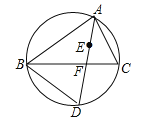
查看答案和解析>>【题目】如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D
(1)求证:△BFD∽△ABD;
(2)求证:DE=DB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.x3?x﹣4=x﹣12
B.(x3)3=x6
C.2x2+x=x
D.(3x)﹣2=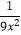
-
科目: 来源: 题型:
查看答案和解析>>【题目】在创建“全国文明城市”和“省级文明城区”过程中,栾城区污水处理厂决定先购买A、B两型污水处理设备共20台,对城区周边污水进行处理.已知每台A型设备价格为12万元,每台B型设备价格为10万元;1台A型设备和2台B型设备每周可以处理污水640吨,2台A型设备和3台B型设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)要想使污水处理厂购买设备的资金不超过230万元,但每周处理污水的量又不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
相关试题

