【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B. 
(1)如图1,直接写出∠A和∠C之间的数量关系;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
参考答案:
【答案】
(1)∠A+∠C=90°;
(2)解:如图2,过点B作BG∥DM,

∵BD⊥AM,
∴DB⊥BG,即∠ABD+∠ABG=90°,
又∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN,
∴∠C=∠CBG,
∴∠ABD=∠C;
(3)解:如图3,过点B作BG∥DM,

∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(2)可得∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,则
∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得
(2α+β)+3α+(3α+β)=180°,①
由AB⊥BC,可得
β+β+2α=90°,②
由①②联立方程组,解得α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.
【解析】(1)根据平行线的性质以及直角三角形的性质进行证明即可;(2)先过点B作BG∥DM,根据同角的余角相等,得出∠ABD=∠CBG,再根据平行线的性质,得出∠C=∠CBG,即可得到∠ABD=∠C;(3)先过点B作BG∥DM,根据角平分线的定义,得出∠ABF=∠GBF,再设∠DBE=α,∠ABF=β,根据∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+3α+(3α+β)=180°,根据AB⊥BC,可得β+β+2α=90°,最后解方程组即可得到∠ABE=15°,进而得出∠EBC=∠ABE+∠ABC=15°+90°=105°.
【考点精析】解答此题的关键在于理解余角和补角的特征的相关知识,掌握互余、互补是指两个角的数量关系,与两个角的位置无关,以及对平行线的判定与性质的理解,了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在∠POQ内部有两点M、N,∠MOP=∠NOQ.
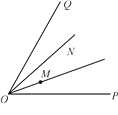
(1)画图并简要说明画法:在射线OP上取一点A,使点A到点M和点N的距离和最小;在射线OQ上取一点B,使点B到点M和点N的距离和最小;
(2)直接写出AM+AN与BM+BN的大小关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆柱的底面直径为6cm,高为10cm,则这个圆柱的侧面积是cm2(结果保留π).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是假命题的是( )
A. 如果a∥b,b∥c,那么a∥c
B. 锐角三角形中最大的角一定大于或等于60°
C. 两条直线被第三条直线所截,内错角相等
D. 矩形的对角线相等且互相平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果代数式3x2+4x=5,则代数式9x2+12x﹣3的值是( )
A. 9 B. 10 C. 11 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】1nm为十亿分之一米,而个体中红细胞的直径约为0.0000077m,那么人体中红细胞直径的纳米数用科学记数法表示为( )
A.7.7×103nmB.7.7×102nm
C.7.7×104nmD.以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题,其中真命题有( )
(1)有理数乘以无理数一定是无理数;
(2)顺次连接等腰梯形各边中点所得的四边形是菱形;
(3)在同圆中,相等的弦所对的弧也相等;
(4)如果正九边形的半径为a,那么边心距为asin20°.
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

