搜索
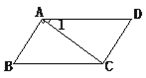
【题目】如图，已知∠1＝30°，∠B＝60°，AB⊥AC。
（1）计算：∠DAB＋∠B
（2）AB与CD平行吗？AD与BC平行吗？
参考答案：
【答案】（1）180°（2）AD∥BC，AB与CD不平行
【解析】试题分析：（1）根据三角形的内角和定理求出∠ACB，根据平行线的判定证出AD∥BC即可；
（2）根据三角形的内角和定理求出∠ACB=∠1，根据平行线的判定即可推出答案．
试题解析：解：（1）∵AB⊥AC，∴∠BAC=90°．∵∠B=60°，∠1=30°，∴∠DAB+∠B=30°+90°+60°=180°．
（2）答：AB与CD不平行．理由是根据已知条件不能推出AB∥CD．
AD与BC平行．理由是：
∵AB⊥AC，∴∠BAC=90°．∵∠B=60°，∠1=30°，∴∠DAB+∠B=30°+90°+60°=180°，∴AD∥BC．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）﹣(﹣3)+7﹣|﹣8|
（2）(﹣1)4﹣8÷(﹣4)×(﹣6+4)
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们规定：三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差．如图1，在△ABC中，AO是BC边上的中线，AB与AC的“极化值”就等于AO2﹣BO2的值，可记为AB△AC=AO2﹣BO2．
（1）在图1中，若∠BAC=90°，AB=8，AC=6，AO是BC边上的中线，则AB△AC= ，OC△OA= ；
（2）如图2，在△ABC中，AB=AC=4，∠BAC=120°，求AB△AC、BA△BC的值；
（3）如图3，在△ABC中，AB=AC，AO是BC边上的中线，点N在AO上，且ON=
AO．已知AB△AC=14，BN△BA=10，求△ABC的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将△ABC沿着射线BC方向平移至△A'B'C'，使点A'落在∠ACB的外角平分线CD上，连结AA'．
（1）判断四边形ACC'A'的形状，并说明理由；
（2）在△ABC中，∠B=90°，A B=24，cos∠BAC=
，求CB'的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某大型超市从生产基地购进一批水果，运输过程中质量损失10%，假设不计超市其他费用，如果超市要想至少获得20%的利润，那么这种水果的售价在进价的基础上应至少提高（ ）
A. 40% B. 33.4% C. 33.3% D. 30
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了顺利通过“国家文明城市”验收，市政府拟对部分路段的人行道地砖、绿化带、排水管等公用设施全面更新改造，根据市政建设的需要，需在40天内完成工程.现有甲、乙两个工程队有意承包这项工程，经调查知道，乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍，若甲、乙两工程队合作只需10天完成.
（1）甲、乙两个工程队单独完成此项工程各需多少天？
（2）若甲工程队每天的费用是4.5万元，乙工程队每天的工程费用是2.5万元，请你设计一种方案，既能按时完成工程，又能使工程费用最少？
-
科目： 来源： 题型：
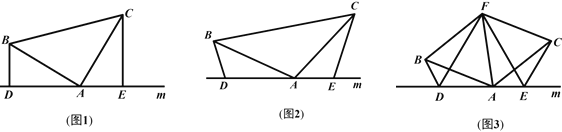
查看答案和解析>>【题目】（1）如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．证明：DE＝BD+CE．
（2）如图2，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？若成立，请给出证明；若不成立，请说明理由．
（3）拓展与应用：如图3，D、E是D、A、E三点所在直线m上的两动点（D、A、E三点
互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA＝∠AEC＝∠BAC，试判断△DEF的形状．
相关试题
