【题目】如图:已知![]() .
.

(1)读句画图:画![]() 的角平分线
的角平分线![]() 、
、![]() 交
交![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() 、
、![]() 交于点
交于点![]() ,过
,过![]() 点作
点作![]() 交
交![]() 的延长线于
的延长线于![]() .
.
(2)在(1)的条件下解决下面问题:
①填表
|
|
|
|
| __________ | ______________ | ______________ |
②根据图中的数据,你发现无论![]() 是什么角,
是什么角,![]() 总是__________(填锐角、钝角或直角).
总是__________(填锐角、钝角或直角).
③若过![]() 点作
点作![]() 于
于![]() ,你能猜想
,你能猜想![]() 与
与![]() 之间的数量关系吗?说明理由.(在(1)中的图上作
之间的数量关系吗?说明理由.(在(1)中的图上作![]() 于
于![]() )
)
参考答案:
【答案】(1)见解析;(2)①![]() ;②锐角;③
;②锐角;③![]() ,理由见解析
,理由见解析
【解析】
(1)根据要求画出图形即可;
(2)①当∠ACB=40°时,根据角平分线定义及三角形外角的性质求出∠AIF,然后可得∠BFC,同理求出其他两种情况;
②根据∠BFC=∠AIF=90°-![]() ∠ACB,得出∠BFC<90°,即可判断;
∠ACB,得出∠BFC<90°,即可判断;
③利用直角三角形两锐角互余可得![]() ,结合
,结合![]() 可得答案.
可得答案.
解:(1)如图所示;
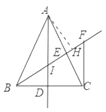
(2)①∵AD,BE是△ABC的角平分线,
∴∠BAI=![]() ∠BAC,∠ABI=
∠BAC,∠ABI=![]() ∠ABC,
∠ABC,
∴∠AIF=∠ABI+∠ABI=![]() (∠BAC+∠ABC)=
(∠BAC+∠ABC)=![]() (180°-∠ACB)=90°-
(180°-∠ACB)=90°-![]() ∠ACB,
∠ACB,
∴当∠ACB=40°时,∠AIF=70°,
∵CF∥AD,
∴∠BFC=∠AIF=70°,
同法可得:当∠ACB=90°时,∠BFC=45°,
当∠ACB=110°时,∠BFC=35°,
故答案为70°,45°,35°;
②∵∠BFC=∠AIF=90°-![]() ∠ACB,
∠ACB,
∴∠BFC<90°,
∴∠BFC总是锐角;
③如图,过![]() 点作
点作![]() 于
于![]() ;
;
结论:![]() ,
,
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
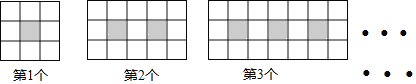
查看答案和解析>>【题目】如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多________个.(用含n的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】A市和B市分别有库存的某联合收割机12台和6台,现决定开往C市10台和D市8台,已知从A市开往C市、D市的油料费分别为每台400元和800元,从B市开往C市和D市的油料费分别为每台300元和500元.
(1)设B市运往C市的联合收割机为x台,求运费w关于x的函数关系式.
(2)若总运费不超过9000元,问有几种调运方案?
(3)求出总运费最低的调运方案,并求出最低运费. -
科目: 来源: 题型:
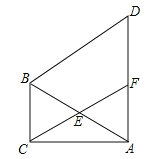
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)若AB=6,求平行四边形BCFD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】乐乐和科学小组的同学们在网上获取了声音在空气中传播的速度与空气温度之间关系的一些数据(如下表)
温度/

-20
-10
0
10
20
30
声速/(
 )
)318
324
330
336
342
348
下列说法中错误的是( )
A.在这个变化过程中,当温度为10
 时,声速是336
时,声速是336
B.温度越高,声速越快
C.当空气温度为20
 时,声音5
时,声音5 可以传播1740
可以传播1740
D.当温度每升高10
 ,声速增加6
,声速增加6
-
科目: 来源: 题型:
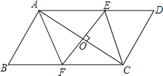
查看答案和解析>>【题目】如图,□ABCD中,AC为对角线,EF⊥AC于点O,交AD于点E,交BC于点F,连结AF、CE.请你探究当O点满足什么条件时,四边形AFCE是菱形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,若CE=2,DF=1,∠EBF=60°,求平行四边形ABCD的面积.
相关试题

