【题目】如图,点C是⊙O的直径AB延长线上的一点,且有BO=BD=BC.
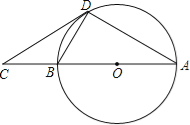
(1)求证:CD是⊙O的切线;
(2)若半径OB=2,求AD的长.
参考答案:
【答案】解:(1)证明:如图,连接OD,
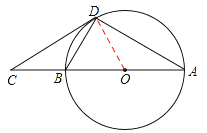
∵BO=BD=DO,∴△OBD是等边三角形。∴∠OBD=∠ODB=60°。
∵BD=BC,∴∠BDC=![]() ∠OBD=30°。
∠OBD=30°。
∴∠ODC=90°。
∴OD⊥CD。
∵OD为⊙O的半径,
∴CD是⊙O的切线。
(2)∵AB为⊙O的直径,∴∠BDA=90°。
∵BO=BD=2,∴AB=2BO=4。
∴![]() 。
。
【解析】试题分析:(1)由于BO=BD=BC,根据等边三角形的判定和性质,三角形外角性质可得∠ODC=90°,从而根据切线的判定方法即可得到结论。
(2)由AB为⊙O的直径得∠BDA=90°,而BO=BD=2, AB=2BO=4,根据勾股定理可求出AD。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求
 的值.
的值.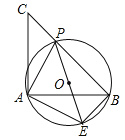
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三个不透明的布袋中分别放入一些除颜色不同外其他都相同的玻璃球,并搅匀,具体情况如下表:

在下列事件中,哪些是随机事件,哪些是必然事件,哪些是不可能事件?
(1) 随机从第一个布袋中摸出一个玻璃球,该球是黄色、绿色或红色的;
(2) 随机的从第二个布袋中摸出两个玻璃球,两个球中至少有一个不是绿色的;
(3) 随机的从第三个布袋中摸出一个玻璃球,该球是红色的;
(4)随机的从第一个布袋中和第二个布袋中各摸出一个玻璃球,两个球的颜色一致.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为
 .
.项目
第一次锻炼
第二次锻炼
步数(步)
10000
____________
平均步长(米/步)
0.6
____________
距离(米)
6000
7020
注:步数×平均步长=距离.
(1)根据题意完成表格填空;
(2)求x;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司对一批某品牌衬衣的质量抽检结果如下表.

(1)从这批衬衣众人抽1件是次品的概率约为多少?
(2)如果销售这批衬衣600件,那么至少要再准备多少件正品衬衣供买到次品的顾客更换?
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2﹣2x=0的解为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.(a2)3=a6
B.a2+a2=a4
C.(3a)(2a)2=6a
D.3a﹣a=3
相关试题

