【题目】如图,在![]() 中,点O是边AC上一个动点,过点O作直线
中,点O是边AC上一个动点,过点O作直线![]() //BC,分别交
//BC,分别交![]() ,外角
,外角![]() 的平分线于点E、F.
的平分线于点E、F.

(1)猜想与证明,试猜想线段OE与OF的数量关系,并说明理由.
(2)连接AE,AF,问:当点O在边AC上运动时到什么位置时,四边形AECF是矩形?并说明理由.
(3)若AC边上存在一点O,使四边形AECF是正方形,猜想![]() 的形状并证明你的结论.
的形状并证明你的结论.
参考答案:
【答案】(1)OE=OF,理由见解析.
(2)当点O在边AC上运动到AC中点时,四边形AECF是矩形;
理由见解析.
(3)△ABC是直角三角形;证明见解析.
【解析】
(1)根据CE平分∠ACB,MN∥BC,找到相等的角,即∠OEC=∠ECB,再根据等边对等角得OE=OC,同理OC=OF,可得EO=FO.
(2)利用矩形的判定解答,即有一个内角是直角的平行四边形是矩形.
(3)利用已知条件及正方形的性质问题可解.
(1)证明:∵CE是∠ACB的平分线,
∴∠ACE=∠BCE,
∵MN∥BC,
∴∠BCE=∠E,
∴∠ACE=∠E,
∴OE=OC,
同理可证OC=OF,
∴OE=OF;
(2)解:如图

当点O在边AC上运动到AC中点时,四边形AECF是矩形.
理由是:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵CE平分∠ACB,CF平分∠ACG,
∴∠ECF=![]() ∠ACB+
∠ACB+![]() ∠ACG=
∠ACG=![]() (∠ACB+∠ACG)=90°,
(∠ACB+∠ACG)=90°,
∴平行四边形AECF是矩形.
(3)△ABC是直角三角形
理由是:∵四边形AECF是正方形,
∴AC⊥EN,故∠AOM=90°,
∵MN∥BC,
∴∠BCA=∠AOM,
∴∠BCA=90°,
∴△ABC是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产
 两种产品共60件,需购买甲、乙两种材料.生产一件
两种产品共60件,需购买甲、乙两种材料.生产一件 产品需甲种材料4千克;生产一件
产品需甲种材料4千克;生产一件 产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产
 产品不少于38件,问符合生产条件的生产方案有哪几种?
产品不少于38件,问符合生产条件的生产方案有哪几种?(3)在(2)的条件下,若生产一件
 产品需加工费40元,生产一件
产品需加工费40元,生产一件 产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D为AB上不与AB重合的一个动点,过点D分别作DE⊥AC于点E,DF⊥BC于点F,则线段EF的最小值为( )

A. 3 B. 4 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F分别为AB、BC上的点,且AE=BF,连结DE、AF,猜想DE、AF的关系并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某家电商场计划用9万元从生产厂家购进50台电视机.已知该厂家生产3种不同型号的电视机,出厂价分别为A种每台1500元,B种每台2100元,C种每台2500元.
(1)若家电商场同时购进两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案;
(2)若商场销售一台A种电视机可获利150元,销售一台B种电视机可获利200元,销售一台C种电视机可获利250元,在同时购进两种不同型号的电视机方案中,为了使销售时获利最多,你选择哪种方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两家汽车销售公司根据近几年的销售量分别制作了如图所示的统计图,从2014~2018年,这两家公司中销售量增长较快的是_____公司(填“甲”或“乙”).
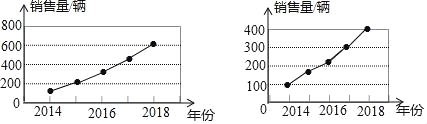
-
科目: 来源: 题型:
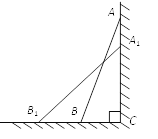
查看答案和解析>>【题目】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米.如果梯子的顶端沿墙面下滑0.4米,那么点B将向左滑动多少米?
相关试题

