【题目】(本题8分)如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.
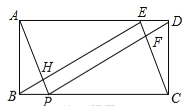
(1)断⊿BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形?并证明你的判断。
参考答案:
【答案】(1)△BEC是直角三角形,理由见解析;
(2)四边形EFPH为矩形,证明见解析;
【解析】
试题分析:(1)由矩形性质得出CD=2,根据勾股定理求出CE和BE,求出CE2+BE2的值,求出BC2,根据勾股定理的逆定理求出即可;
(2)由矩形的性质和平行四边形的判定,推出平行四边形DEBP和AECP,推出EH∥FP,EF∥HP,推出平行四边形EFPH,根据矩形的判定推出即可;
试题解析:(1)△BEC是直角三角形,
理由是:∵矩形ABCD,
∴∠ADC=∠ABP=90°,AD=BC=5,AB=CD=2,
由勾股定理得:CE=![]() ,
,
同理BE=2![]() ,
,
∴CE2+BE2=5+20=25,
∵BC2=52=25,
∴BE2+CE2=BC2,
∴∠BEC=90°,
∴△BEC是直角三角形.
(2)四边形EFPH为矩形,
∵矩形ABCD,
∴AD=BC,AD∥BC,
∵DE=BP,
∴四边形DEBP是平行四边形,
∴BE∥DP,
∵AD=BC,AD∥BC,DE=BP,
∴AE=CP,
∴四边形AECP是平行四边形,
∴AP∥CE,
∴四边形EFPH是平行四边形,
∵∠BEC=90°,
∴平行四边形EFPH是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求代数式(
 ﹣
﹣  )÷
)÷ 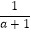 的值,其中a=2sin60°+tan45°.
的值,其中a=2sin60°+tan45°. -
科目: 来源: 题型:
查看答案和解析>>【题目】海静中学开展以“我最喜爱的职业”为主题的调查活动,围绕“在演员、教师、医生、律师、公务员共五类职业中,你最喜爱哪一类?(必选且只选一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:

(1)本次调查共抽取了多少名学生?
(2)求在被调查的学生中,最喜爱教师职业的人数,并补全条形统计图;
(3)若海静中学共有1500名学生,请你估计该中学最喜爱律师职业的学生有多少名? -
科目: 来源: 题型:
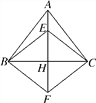
查看答案和解析>>【题目】如图,在等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
(1)求证:四边形EBFC是菱形;
(2)如果∠BAC=∠ECF,求证:AC⊥CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.
(1)求A、B两种学习用品的单价各是多少元?
(2)若购买这批学习用品的费用不超过28000元,则最多购买B型学习用品多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.

(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个饭店所有员工的月收入情况如下:

你认为用来描述该饭店员工的月收入水平不太恰当的是( )
A. 所有员工月收入的平均数
B. 所有员工月收入的中位数
C. 所有员工月收入的众数
D. 所有员工月收入的中位数或众数
相关试题

