【题目】一次函数y=kx+b(k≠0)的图象经过点A(2,-6),且与反比例函数y=-![]() 的图象交于点B(a,4)
的图象交于点B(a,4)
(1)求一次函数的解析式;
(2)将直线AB向上平移10个单位后得到直线l:y1=k1x+b1(k1≠0),l与反比例函数y2= ![]() 的图象相交,求使y1<y2成立的x的取值范围.
的图象相交,求使y1<y2成立的x的取值范围.
参考答案:
【答案】(1)一次函数的解析式为y=-2x-2.(2)
【解析】
试题分析:(1)根据点B的纵坐标利用反比例函数图象上点的坐标特征可求出点B的坐标,根据点A、B的坐标利用待定系数法即可求出直线AB的解析式;
(2)根据“上加下减”找出直线l的解析式,联立直线l和反比例函数解析式成方程组,解方程组可找出交点坐标,画出函数图象,根据两函数图象的上下位置关系即可找出使y1<y2成立的x的取值范围.2-
试题解析:(1)∵反比例函数y=-![]() 的图象过点B(a,4),
的图象过点B(a,4),
∴4=-![]() ,解得:a=-3,
,解得:a=-3,
∴点B的坐标为(-3,4).
将A(2,-6)、B(-3,4)代入y=kx+b中,
![]() ,解得:
,解得: ![]() ,
,
∴一次函数的解析式为y=-2x-2.
(2)直线AB向上平移10个单位后得到直线l的解析式为:y1=-2x+8.
联立直线l和反比例函数解析式成方程组,
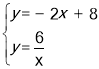 ,解得:
,解得:![]() ,
,![]() ,
,
∴直线l与反比例函数图象的交点坐标为(1,6)和(3,2).
画出函数图象,如图所示.

观察函数图象可知:当0<x<1或x>3时,反比例函数图象在直线l的上方,
∴使y1<y2成立的x的取值范围为0<x<1或x>3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,交AD于E,若AE=13,求AF的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知当x=1时,ax2﹣bx的值为10,则当x=﹣1时,ax2+bx的值为( )
A. 1B. ﹣1C. 10D. ﹣10
-
科目: 来源: 题型:
查看答案和解析>>【题目】成都地铁自开通以来,发展速度不断加快,现已成为成都市民主要出行方式之一.今年4月29日成都地铁安全运输乘客约181万乘次,又一次刷新客流纪录,这也是今年以来第四次客流纪录的刷新,用科学记数法表示181万为( )
A.18.1×105
B.1.81×106
C.1.81×107
D.181×104 -
科目: 来源: 题型:
查看答案和解析>>【题目】|﹣2019|=_____.
-
科目: 来源: 题型:
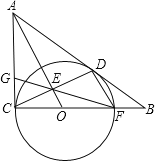
查看答案和解析>>【题目】如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.
(1)求证:DF∥AO;
(2)若AC=6,AB=10,求CG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)若3a=6,9b=2,求32a+4b的值;
(2)已知xy=8,x﹣y=2,求代数式 x3y﹣x2y2+
x3y﹣x2y2+  xy3的值.
xy3的值.
相关试题

