【题目】小丽一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L,行驶ah后,途中在加油站加油若干bL.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示.根据图象回答下列问题:
①小汽车行驶________h后加油, 中途加油__________L;
②求加油前油箱余油量Q与行驶时间t的函数关系式;
③如果加油站距景点200km,车速为80km/h,要到达目的
地,油箱中的油是否够用?请说明理由。

参考答案:
【答案】(1)3h ,24L(2)Q=-10t+36(0≤t≤3)(3)邮箱中的油是够用的
【解析】分析:(1)观察图中数据可知,行驶3小时后油箱剩油6L,加油加至30L;
(2)先根据图中数据把每小时用油量求出来,即:(36-6)÷3=10L,再写出函数关系式;
(3)先要求出从加油站到景点需行几小时,然后再求需用多少油,便知是否够用.
详解:(1)从图中可知汽车行驶3h后加油,中途加油24L;
(2)根据分析可知Q=-10t+36(0≤t≤3);
(3)油箱中的油是够用的.
∵200÷80=2.5(小时),需用油10×2.5=25L<30L,
∴油箱中的油是够用的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,点E是BC边上一动点(不与B、C重合).连接AE,过点E作EF⊥AE,交DC于点F.

(1)求证:△ABE∽△ECF;
(2)连接AF,试探究当点E在BC什么位置时,∠BAE=∠EAF,请证明你的结论. -
科目: 来源: 题型:
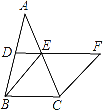
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在不透明的箱子里放有4个乒乓球,每个乒乓球上分别写有数字1、2、3、4,从箱中摸出一个球记下数字后放回箱中,摇匀后再摸出一个记下数字.若将第一次摸出的球上的数字记为点的横坐标,第二次摸出球上的数字记为点的纵坐标.
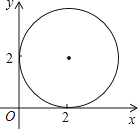
(1)请用列表法或树状图法写出两次摸球后所有可能的结果.
(2)求这样的点落在如图所示的圆内的概率(注:图中圆心在直角坐标系中的第一象限内,并且分别于x轴、y轴切于点(2,0)和(0,2)两点). -
科目: 来源: 题型:
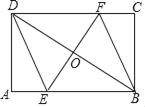
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,过对角线BD的中点O的直线分别交AB、CD于点E、F,连接DE,BF.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)体育课上,某中学对七年级男生进行了引体向上测试,以能做7个为标准多于标准的次
数记为正数,不足的次数记为负数,其中8名男生的成绩为+2,-1,+3,0,-2,-3,+1,0.
(1)这8名男生中达到标准的占百分之几?
(2)他们共做了多少次引体向上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知P为⊙O外一点,PA为⊙O的切线,B为⊙O上一点,且PA=PB,C为优弧
 上任意一点(不与A、B重合),连接OP、AB,AB与OP相交于点D,连接AC、BC.
上任意一点(不与A、B重合),连接OP、AB,AB与OP相交于点D,连接AC、BC.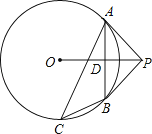
(1)求证:PB为⊙O的切线;
(2)若tan∠BCA= ,⊙O的半径为
,⊙O的半径为 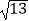 ,求弦AB的长.
,求弦AB的长.
相关试题

