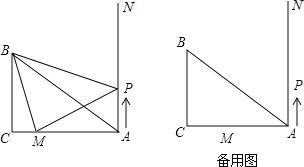
【题目】如图,在 Rt△ABC 中,∠C=90°,AC=8cm,BC=6cm,M 在 AC上,且AM=6cm,过点 A(与 BC 在 AC 同侧)作射线 AN⊥AC,若动点 P 从点 A 出发,沿射线 AN 匀速运动,运动速度为 1cm/s,设点 P 运动时间为 t 秒.
(1)经过 秒时,Rt△AMP 是等腰直角三角形?
(2)经过几秒时,PM⊥MB?
(3)经过几秒时,PM⊥AB?
(4)当△BMP 是等腰三角形时,直接写出 t 的所有值.
参考答案:
【答案】(1)6;(2)2;(3)8;(4)2或![]() .
.
【解析】
(1)得出腰时AM=AP,即可得出答案;
(2)根据垂直的定义和同角的余角相等得到∠CBM=∠AMP,证明△CBM≌△AMP,根据全等三角形的性质得到 AP=CM=2,根据题意得到答案;
(3)证明△APM≌△CAB,根据全等三角形的性质得到 AP=CA=8,根据题意得到答案;
(4)分 MB=MP 和 PB=PM 两种情况,根据全等三角形的性质,勾股定理计算即可.
(1)当 Rt△AMP 是等腰直角三角形时,AP=AM=6cm,
∴t=6÷1=6(s),
故答案为:6;
(2)当 PM⊥MB 时,∠BMP=90°,
∴∠BMC+∠AMP=90°,又∠BMC+∠CBM=90°,
∴∠CBM=∠AMP,
在△CBM 和△AMP 中,
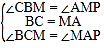 ,
,
∴△CBM≌△AMP(ASA),
∴AP=CM=2,
∴t=2,即经过 2 秒时,PM⊥MB;
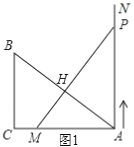
(3)当 PM⊥AB 时,如图1,∠PHA=90°,
∴∠HPA+∠HAP=90°,又∠HAP+∠CAB=90°,
∴∠APM=∠CAB,
在△APM 和△CAB 中,
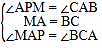 ,
,
∴△APM≌△CAB(ASA),
∴AP=CA=8,
∴t=8,
∴经过 8 秒时,PM⊥AB;
(4)根据勾股定理得,BM=![]() ,BP 的最小值为 8,
,BP 的最小值为 8,
∵![]() <8,
<8,
∴BM≠BP,
当 MB=MP 时,
在 Rt△BCM 和 Rt△MAP 中,
![]() ,
,
∴Rt△BCM≌Rt△MAP(HL),
∴AP=CM=2, 则 t=2,
当 PB=PM 时,如图2,作BF⊥AN于 F, 则四边形 BCAF 为矩形,
∴BF=CA=8,AF=BC=6,
∴PF=6﹣t,
由勾股定理得,BP2=PF2+BF2,MP2=AM2+AP2,
∴PF2+BF2=AM2+AP2,即(6﹣t)2+82=62+t2, 解得,t=![]() ,
,
∴当△BMP 是等腰三角形时,t=2 或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上两点A、B所表示的数分别为-3、1.
(1)写出线段AB的中点M所对应的数;
(2)若点P从B出发,以每秒2个单位长度的速度向左运动,运动时间为
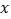 秒:
秒:①用含
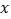 的代数式表示点P所对应的数;
的代数式表示点P所对应的数;②当BP=2AP时,求
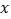 值。
值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=2,BF=8,BC=AE=6,CE=CF=7,则△CDF与四边形ABDE的面积比值是( )
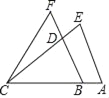
A. 1:1 B. 2:1 C. 1:2 D. 2:3
-
科目: 来源: 题型:
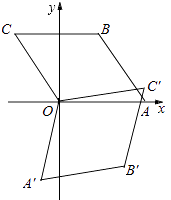
查看答案和解析>>【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )
A.(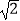 ,﹣
,﹣ 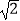 )
)
B.(﹣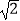 ,
, 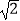 )
)
C.(2,﹣2)
D.(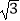 ,﹣
,﹣ 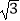 )
) -
科目: 来源: 题型:
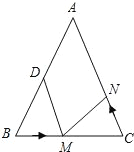
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=12厘米,BC=8厘米,点D为AB的中点,如果点M在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点N在线段CA上由C点向A点运动,若使△BDM与△CMN全等,则点N的运动速度应为_____厘米/秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连结对角线相等的四边形的四边中点所得图形是( )
A.正方形
B.矩形
C.菱形
D.以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】补全下列解题过程:
如图,OD是∠AOC的平分线,且∠BOC-∠AOB=40°,若∠AOC=120°,求∠BOD的度数.
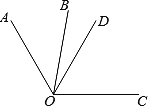
解:∵OD是∠AOC的平分线,∠AOC=120°
∴∠DOC=
 ∠_______=______°.
∠_______=______°.∵∠BOC+∠_____=120°,∠BOC-∠AOB=40°
∴∠BOC=80°
∴∠BOD=∠BOC-∠______=______°
相关试题

