搜索
【题目】如图，△COD是△AOB绕点O顺时针旋转40°后得到的图形，若点C恰好落在AB上，且∠AOD的度数为90°，则∠B的度数是 ． 
参考答案：
【答案】60°
【解析】解：∵△COD是△AOB绕点O顺时针旋转40°后得到的图形， ∴∠AOC=∠BOD=40°，AO=CO，
∵∠AOD=90°，
∴∠BOC=90°﹣40°×2=10°，
∠ACO=∠A= 
（180°﹣∠AOC）= （180°﹣40°）=70°，
由三角形的外角性质得，∠B=∠ACO﹣∠BOC=70°﹣10°=60°．
故答案为：60°．
根据旋转的性质可得∠AOC=∠BOD=40°，AO=CO，再求出∠BOC，∠ACO，然后利用三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．
-
科目： 来源： 题型：
查看答案和解析>>【题目】按图填空，并注明理由．
⑴完成正确的证明：如图，已知AB∥CD，求证：∠BED=∠B+∠D
证明：过E点作EF∥AB（经过直线外一点有且只有一条直线与这条直线平行）
∴∠1= （ ）
∵AB∥CD（已知）
∴EF∥CD（如果两条直线与同一直线平行，那么它们也平行）
∴∠2= （ ）
又∠BED=∠1+∠2
∴∠BED=∠B+∠D （等量代换）．
⑵如图，在△ABC中，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．
解：因为EF∥AD（已知）
所以∠2=∠3．（ ）
又因为∠1=∠2，所以∠1=∠3．（等量代换）
所以AB∥ （ ）
所以∠BAC+ =180°（ ）．
又因为∠BAC=70°，所以∠AGD=110°．
图⑴ 图⑵
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，已知AB＝AC，∠BAC和∠ACB的平分线相交于点D，∠ADC＝125°，求∠ACB和∠BAC的度数．
-
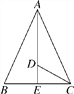
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC的边BC=2
cm，且△ABC内接于半径为2cm的⊙O，则∠A=度． -
科目： 来源： 题型：
查看答案和解析>>【题目】有一天李小虎同学用“几何画板”画图，他先画了两条平行线AB，CD，然后在平行线间画了一点E，连接BE，DE后（如图①），他用鼠标左键点住点E，拖动后，分别得到如图②，③，④等图形，这时他突然一想，∠B，∠D与∠BED之间的度数有没有某种联系呢？接着小虎同学通过利用“几何画板”的“度量角度”和“计算”功能，找到了这三个角之间的关系．
（1）你能探究出图①到图④各图中的∠B，∠D与∠BED之间的关系吗？
（2）请从所得的四个关系中，选一个说明它成立的理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知AB是⊙O的直径，弦CD⊥AB于点E，弦PQ∥AB交弦CD于点M，BE=18，CD=PQ=24，则OM的长为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，点D、E、F分别在三边上，E是AC的中点，AD、BE、CF交于一点G，BD=2DC，S△GEC=3，S△GDC=4，则△ABC的面积是_____．
相关试题
