【题目】如图,过点A(2,0)的两条直线l1 , l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB= ![]() .
. 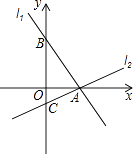
(1)求点B的坐标;
(2)若△ABC的面积为4,求直线l2的解析式.
参考答案:
【答案】
(1)解:∵点A(2,0),AB= ![]()
∴BO= ![]() =
= ![]() =3
=3
∴点B的坐标为(0,3)
(2)解:∵△ABC的面积为4
∴ ![]() ×BC×AO=4
×BC×AO=4
∴ ![]() ×BC×2=4,即BC=4
×BC×2=4,即BC=4
∵BO=3
∴CO=4﹣3=1
∴C(0,﹣1)
设l2的解析式为y=kx+b,则
![]() ,解得
,解得 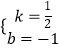
∴l2的解析式为y= ![]() x﹣1
x﹣1
【解析】(1)先根据勾股定理求得BO的长,再写出点B的坐标;(2)先根据△ABC的面积为4,求得CO的长,再根据点A、C的坐标,运用待定系数法求得直线l2的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“神十”圆满完成载人航天飞行任务后,专家将对返回舱零部件进行检查,应采取的合理的调查方式是____.
-
科目: 来源: 题型:
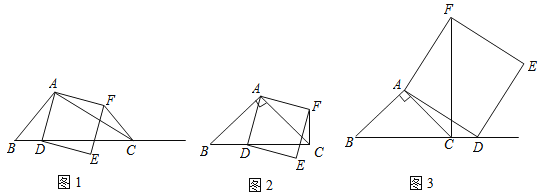
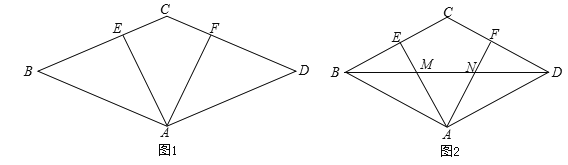
查看答案和解析>>【题目】在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.如果AB=AC,∠BAC=90o,
(1)当点D在线段BC上时(与点B不重合),如图2,线段CF 、BD所在直线的位
置关系为 __________,线段CF 、BD的数量关系为 ;
(2)当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在菱形ABCD中,AE⊥BC,AF⊥CD,垂足为E、F.
(1)求证:△ABE≌△ADF;
(2)若∠BAE=∠EAF,求证:AE=BE;
(3)若对角线BD与AE、AF交于点M、N,且BM=MN(如图2),求证:∠EAF=2∠BAE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)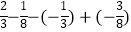
(2)6.25×(﹣3.4)+6.25×4.4
(3)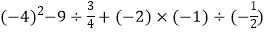
(4)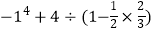
(5)(﹣1)2015﹣(1﹣0.5)2×|2﹣22|
(6)﹣1+2﹣3+4﹣…﹣2015+2016. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,这是一个由小立方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,请你画出它的正视图与左视图.
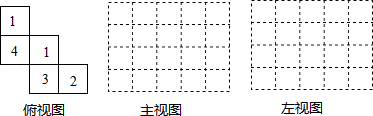
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
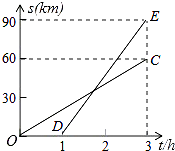
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
相关试题

