搜索
【题目】已知：如图，ABCD中，CD=CB=2，∠C=60°，点E是CD边上自D向C的动点（点E运动到点C停止运动），连结AE，以AE为一边作等边△AEP，连结DP． 
（1）求证：△ABE≌△ADP；
（2）点P随点E的运动而运动，请直接写出点P的运动路径长 ．
参考答案：
【答案】
（1）证明：在ABCD中，
∵BC=CD，
∴ABCD是菱形，
∴AB=AD，
∵△AEP是等边三角形，
∴AP=AE，∠PAE=60°，
∵∠BAD=∠C=60°，
∴∠PAE=∠DAB，
∴∠PAE﹣∠DAE=∠DAB﹣∠DAE，
即∠1=∠2，
在△ABE与△ADP中，
，
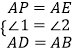∴△ABE≌△ADP（SAS）
（2）2
【解析】（2）解：∵点E在CD边上自D向C的运动， ∴点E的运动路径长是2，
∴点P的运动路径长为：2．
所以答案是：2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC和△BCD都是等边三角形，连接BE、AD交于O．
求证：（1）AD=BE （2）∠AOB=60°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市某幼儿园六一期间举行亲子游戏，主持人请三位家长分别带自己的孩子参加游戏，主持人准备把家长和孩子重新组合完成游戏，A、B、C分别表示三位家长，他们的孩子分别对应的是a、b、c．
（1）若主持人分别从三位家长和三位孩子中各选一人参加游戏，恰好是A、a的概率是多少（直接写出答案）
（2）若主持人先从三位家长中任选两人为一组，再从孩子中任选两人为一组，四人共同参加游戏，恰好是两对家庭成员的概率是多少．（画出树状图或列表） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
，BE平分
，
．
与BC平行吗？请说明理由；
与EF的位置关系如何？为什么？解：
理由如下：
平角的定义
已知
______
______
______与EF的位置关系是______
平分
已知
角平分线的定义又
，已知即
______等量代换
______
______
-
科目： 来源： 题型：
查看答案和解析>>【题目】某超市用5000元购进一批儿童玩具进行试销，很快销售一空．于是超市又调拨18000元资金购进该种儿童玩具，这次进货价比试销时每件多1元，购进的数量是试销时购进数量的3倍．
（1）求试销时该种儿童玩具每件进货价是多少元？
（2）超市将第二批儿童玩具按照试销时的标价出售90%后，余下的八折售完．试销和第二批儿童玩具两次销售中，超市总盈利不少于8520元，那么该种儿童玩具试销时每件标价至少为多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在城镇化建设中，开发商要处理A地大量的建筑垃圾，A地只能容纳1台装卸机作业，装卸机平均每6分钟可以给工程车装满一车建筑垃圾，每辆工程车要将建筑垃圾运送至20千米的B处倾倒，每次倾倒时间约为1分钟，倾倒后立即返回A地等候下一次装运，直到装运完毕；工程车的平均速度为40千米/时．
（1）一辆工程车运送一趟建筑垃圾（从装车到返回）需要多少分钟？
（2）至少安排多少辆工程车既能保证装卸机不空闲，又能保证工程车最少等候时间？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，点E是边BC的中点，DE的延长线与AB的延长线相交于点F.
（1）求证：△CDE≌△BFE；
（2）试连接BD、CF，判断四边形CDBF的形状，并证明你的结论
相关试题
