【题目】如图,点E为正方形ABCD的边BC所在直线上的一点,连接AE,过点C作CF⊥AE于F,连接BF.

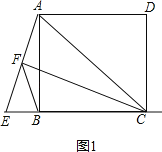
(1)如图1,当点E在CB的延长线上,且AC=EC时,求证:BF=![]() ;
;
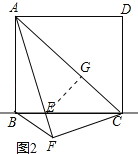
(2)如图2,当点E在线段BC上,且AE平分∠BAC时,求证:AB+BE=AC;
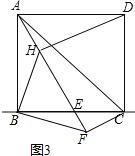
(3)如图3,当点E继续往右运动到BC中点时,过点D作DH⊥AE于H,连接BH.求证:∠BHF=45°.
参考答案:
【答案】见解析
【解析】
试题分析:(1)根据等腰三角形的性质和直角三角形斜边中线的性质即可证得结论;
(2)作EG⊥AC于G,根据角平分线的性质得出BE=EG,进而通过RT△ABE≌RT△AGE得出AG=AB,然后证得△EGC是等腰直角三角形,从而证得EG=GC,即可证得AB+BE=AC;
(3)设正方形的边长为1,则AB=AD=1,BE=EC=![]() ,根据勾股定理求得AE=
,根据勾股定理求得AE=![]() ,然后通过证得△AEB∽△CEF,△ADH∽△EAB,对应边成比例证得CF=AH=
,然后通过证得△AEB∽△CEF,△ADH∽△EAB,对应边成比例证得CF=AH=![]() ,然后根据SAS证得△ABH≌△CBF,证得BH=BF,∠ABH=∠CBF,从而证得△HBF是等腰直角三角形,从而证得∠BHF=45°.
,然后根据SAS证得△ABH≌△CBF,证得BH=BF,∠ABH=∠CBF,从而证得△HBF是等腰直角三角形,从而证得∠BHF=45°.
(1)证明:如图1,∵AC=EC,CF⊥AE,
∴AF=EF,
∴BF是RT△ABE的斜边的中线,
∴BF=![]() AE;
AE;
(2)如图2,作EG⊥AC于G,
∵AE平分∠BAC,AB⊥BE,
∴BE=EG,
在RT△ABE和RT△AGE中
![]() ,
,
∴RT△ABE≌RT△AGE(HL),
∴AG=AB,
∵四边形ABCD是正方形,
∴∠ACB=45°,
∴∠GEC=45°,
∴∠GEC=∠ACB=45°,
∴EG=GC,
∴AB+BE=AG+GC,
即AB+BE=AC;
(3)如图3,设正方形的边长为1,则AB=AD=1,
∵点E是BC中点,
∴BE=EC=![]() ,
,
∴AE=![]() =
=![]() ,
,
∵∠ABE=∠CFE=90°,∠AEB=∠CEF,
∴△AEB∽△CEF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CF=![]() ,
,
∵AD∥BC,
∴∠DAH=∠AEB,
∵∠AHD=∠BEA=90°,
∴△ADH∽△EAB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AH=![]() ,
,
∴CF=AH,
在△ABH和△CBF中
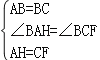
∴△ABH≌△CBF(SAS),
∴BH=BF,∠ABH=∠CBF,
∵∠ABH+∠HBE=∠ABE=90°,
∴∠HBF=90°,
∴△HBF是等腰直角三角形,
∴∠BHF=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点P(﹣2,1)关于y轴对称点P的坐标是( )
A. (﹣2,1) B. (2,﹣1) C. (﹣2,﹣1) D. (2,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=5是关于x的方程2x+3m﹣1=0的解,则m的值为( )
A. 0 B. ﹣1 C. ﹣2 D. ﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,直线PA交⊙O于A、E两点,PA的垂线DC切⊙O于点C,过A点作⊙O的直径AB.

(1)求证:AC平分∠DAB;
(2)若DC=4,DA=2,求⊙O的直径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程x2﹣2(2﹣k)x+k2+12=0有实数根α、β.
(1)求实数k的取值范围;
(2)设
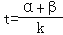 ,求t的最小值.
,求t的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2015年“中国好声音”全国巡演重庆站在奥体中心举行.童童从家出发前往观看,先匀速步行至轻轨车站,等了一会儿,童童搭乘轻轨至奥体中心观看演出,演出结束后,童童搭乘邻居刘叔叔的车顺利到家.其中x表示童童从家出发后所用时间,y表示童童离家的距离.下图能反映y与x的函数关系式的大致图象是( )
A.
 B.
B.  C.
C. 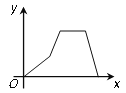 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在国家政策的宏观调控下,某市的商品房成交价由今年3月份的14000元/m2下降到5月份的12600元/m2
(1)问4、5两月平均每月降价的百分率是多少?(参考数据:
 ≈0.95)
≈0.95)(2)如果房价继续回落,按此降价的百分率,你预测到7月份该市的商品房成交均价是否会跌破10000元/m2?请说明理由.
相关试题

