Question

【题目】如图，在平面直角坐标系中，O为原点，直线AB分别与x轴、y轴交于B和A，与反比例函数的图象交于C、D，CE⊥x轴于点E，tan∠ABO=，OB=4，OE=2．

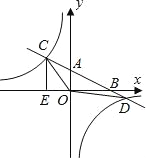
（1）求直线AB和反比例函数的解析式；

（2）求△OCD的面积．

Answer 1

【答案】（1）直线AB的解析式为y=-x+2．反比例函数的解析式为y=-．（2）8.

【解析】

试题分析：（1）根据已知条件求出A、B、C点坐标，用待定系数法求出直线AB和反比例的函数解析式；

（2）联立一次函数的解析式和反比例的函数解析式可得交点D的坐标，从而根据三角形面积公式求解．

试题解析：（1）∵OB=4，OE=2，

∴BE=2+4=6．

∵CE⊥x轴于点E，tan∠ABO=．

∴OA=2，CE=3．

∴点A的坐标为（0，2）、点B的坐标为C（4，0）、点C的坐标为（-2，3）．

设直线AB的解析式为y=kx+b，则，

解得．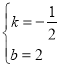

故直线AB的解析式为y=-x+2．

设反比例函数的解析式为y=（m≠0），

将点C的坐标代入，得3=，

∴m=-6．

∴该反比例函数的解析式为y=-．

（2）联立反比例函数的解析式和直线AB的解析式可得

，

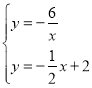可得交点D的坐标为（6，-1），

则△BOD的面积=4×1÷2=2，

△BOC的面积=4×3÷2=6，

故△OCD的面积为2+6=8．