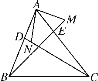
【题目】如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是________.
参考答案:
【答案】90°
【解析】
只要证明△ABM≌△NCA,可得∠BAM=∠CNA,由∠CNA=∠ADC+∠BAN=90°+∠BAN,∠BAM=∠MAN+∠BAN,即可推出∠MAN=90°.
∵CD、BE是边AB和AC上的高,
∴∠ADC=∠AEB=90°,
∴∠ABM+∠BAC=90°,∠BAC+∠ACN=90°,
∴∠ABM=∠ACN,
在△ABM和△ACN中,
∵AB=CN,∠ABM=∠CAN,BM=AC,
∴△ABM≌△NCA,
∴∠BAM=∠CNA,
∵∠CNA=∠ADC+∠BAN=90°+∠BAN,∠BAM=∠MAN+∠BAN,
∴∠MAN=90°.
故答案为90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE,CF交于点D,则下列结论中不正确的是( )

A. △ABE≌△ACF B. 点D在∠BAC的平分线上
C. △BDF≌△CDE D. D是BE的中点
-
科目: 来源: 题型:
查看答案和解析>>【题目】两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小詹在探究筝形的性质时,得到如下结论:

①AC⊥BD;②AO=CO;③△ABD≌△CBD.
其中正确的结论有( )
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若一个三位数的十位上数字为7,且从4、5、6、8中随机选取两数,与7组成“中高数”,那么组成“中高数”的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:

(1)△AEF≌△CEB;
(2)AF=2CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某容器由A、B、C三个连通长方体组成,其中A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是整个容器容积的
 (容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.
(容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.(1)求注满整个容器所需的总时间;
(2)设容器A的高度为xcm,则容器B的高度为 cm;
(3)求容器A的高度和注水的速度.

-
科目: 来源: 题型:
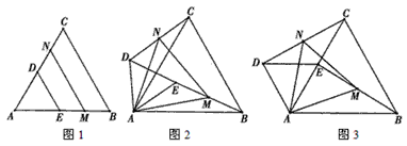
查看答案和解析>>【题目】如图,若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形.
(1)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由;
(2)当△ADE绕A点旋转到图3的位置时,△AMN是否还是等边三角形?若是,请给出证明;若不是,请说明理由.
相关试题

