搜索
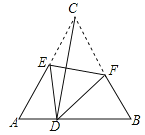
【题目】如图，D是等边△ABC边AB上的一点，且AD：DB＝1：2，现将△ABC折叠，使点C与D重合，折痕为EF，点E、F分别在AC和BC上，则CE：CF的值为（ ）
A. 
B. 
C. 
D. 
参考答案：
【答案】A
【解析】解：由折叠的性质可得，∠EDF=∠C=60，CE=DE，CF=DF．∵∠BDF+∠ADE=∠BDF+∠BFD=120，∴∠ADE=∠BFD，又∵∠A=∠B=60，∴△AED∽△BDF，∴ 
，设AD=a，BD=2a，AB=BC=CA=3a，再设CE==DE=x，CF==DF=y，则AE=3a-x，BF=3a-y，所以
，整理可得ay=3ax-xy，2ax=3ay-xy，即xy=3ax-ay①，xy=3ay-2ax②；把①代入②可得3ax-ay=3ay-2ax，所以5ax=4ay， 
，即
，故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD的对角线AC，BD相交于点O，点E，F在BD上，BE=DF．
（1）求证：AE=CF；
（2）若AB=6，∠COD=60°，求矩形ABCD的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，三角形DEF是三角形ABC经过某种变换得到的图形，点A与点D、点B与点E、点C与点F分别是对应点．观察点与点的坐标之间的关系，解答下列问题：
(1)分别写出点A与点D、点B与点E、点C与点F的坐标，并说出三角形DEF是由三角形ABC经过怎样的变换得到的；
(2)若点Q(a＋3，4－b)是点P(2a，2b－3)通过上述变换得到的，求a－b的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，AC=3cm，BC=4cm. P、Q分别为AB、BC上的动点，点P从点A出发沿AB方向作匀速移动的同时，点Q从点B出发沿BC方向向点C作匀速移动，移动的速度均为1cm/s，设P、Q移动的时间为t（0＜t≤4）.
（1）当t为何值时，△BPQ与△ABC相似；
（2）当t为何值时，△BPQ是等腰三角形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点A（﹣1，﹣2），点B（1，4）
（1）试建立相应的平面直角坐标系；
（2）描出线段AB的中点C，并写出其坐标；
（3）将线段AB沿水平方向向右平移3个单位长度得到线段A1B1，写出线段A1B1两个端点及线段中点C1的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】近年来，由于土地沙化日渐加剧，沙尘暴频繁，严重影响国民生活．为了解某地区土地沙化情况，环保部门对该地区进行了连续四年跟踪观测，所记录的近似数据如下表：
观测时间
第1年
第2年
第3年
第4年
沙漠面积
90万亩
90.2万亩
90.4万亩
90.6万亩
（1）根据表中提供的信息，在不采取任何措施的情况下，试定出该地区沙漠面积y（万亩）与x（年数）之间的关系式（用含x的式子表示y），并计算到第20年时该地区的沙漠面积；
（2）为了防沙治沙，政府决定投入资金，鼓励农民植树种草，经测算，植树1亩需资金200元，种草1亩需资金100元．某组农民计划在一年内完成2400亩绿化任务．在实施中，由于实际情况所限，植树完成了计划的90%，种草超额完成了计划的20%，恰好完成了计划的绿化任务，那么所节余的资金还能植树多少亩？
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于x的一元二次方程
有两个不相等的实数根
、
．（1）求实数k的取值范围．（2）若方程的两个实数根
、
满足
，求k的值．
相关试题
