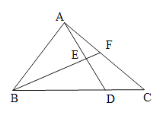
【题目】如图,△ABC的面积为40cm2,AE=ED,BD=3DC,则图中△AEF的面积等于______cm2.
参考答案:
【答案】![]()
【解析】
连接DF,根据AE=ED,BD=3DC,可知S△AEF=S△EFD,S△ABE=S△BED,S△BDF=3S△FDC,S△ABD=3S△ADC,从而求得S△BDE=15,设△AEF面积为x,根据△ABC的面积等于40cm2即可列方程x+x+ S△BDE + S△BDE +![]() (x+ S△BDE)=40,解方程即可.
(x+ S△BDE)=40,解方程即可.
如图,连接DF,
∵AE=ED,BD=3DC,
∴S△AEF=S△EFD,S△ABE=S△BED,S△BDF=3S△FDC,S△ABD=3S△ADC,
又∵△ABC的面积为40cm2,
∴S△ABD=3S△ADC=30,
又∵AE=ED,
∴S△BDE=15,
设△AEF面积为x,
则x+x+ S△BDE + S△BDE +![]() (x+ S△BDE)=40,
(x+ S△BDE)=40,
解得x=![]() .
.
故答案是:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)画一个△BCP(要求各顶点在格点上,P不与A点重合),使其面积等于△ABC的面积.并回答,满足这样条件的点P共________个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A,B两点分别在x轴和y轴上,OA=1,OB=
 ,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1 , 连接A1B1 , 再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 .
,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1 , 连接A1B1 , 再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,BD是△ABC的角平分线,P是射线AC上任意一点 (不与A、D、C三点重合),过点P作PQ⊥AB,垂足为Q,交线段BD于E.
(1)如图①,当点P在线段AC上时,说明∠PDE=∠PED.
(2)画出∠CPQ的角平分线交线段AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E,F,与双曲线y=﹣
 (x<0)交于点P(﹣1,n),且F是PE的中点,直线x=a与l交于点A,与双曲线交于点B(不同于A),PA=PB,则a= .
(x<0)交于点P(﹣1,n),且F是PE的中点,直线x=a与l交于点A,与双曲线交于点B(不同于A),PA=PB,则a= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AOB和△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒20°的速度沿顺时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣
 )﹣2﹣|﹣
)﹣2﹣|﹣ 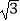 |+2sin60°+(π﹣4)0 .
|+2sin60°+(π﹣4)0 .
相关试题

