【题目】如图,在菱形ABCD中,∠A=110°,E , F分别是边AB和BC的中点,EP⊥CD于点P , 求∠FPC . 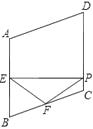
参考答案:
【答案】解答:解:延长PF交AB的延长线于点G , ,在△BGF与△CPF中, 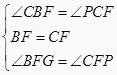 ,∴△BGF≌△CPF , ∴GF=PF , ∴F为PG中点.又∵EP⊥CD , ∴∠BEP=90°,∴EF=
,∴△BGF≌△CPF , ∴GF=PF , ∴F为PG中点.又∵EP⊥CD , ∴∠BEP=90°,∴EF= ![]() PG ,
PG ,
∵PF= ![]() PG(中点定义),∴EF=PF , ∴∠FEP=∠EPF , ∵∠BEP=∠EPC=90°,∴∠BEP-∠FEP=∠EPC-∠EPF , 即∠BEF=∠FPC , ∵四边形ABCD为菱形,∴AB=BC , ∠ABC=180°-∠A=70°,∵E , F分别为AB , BC的中点,∴BE=BF , ∠BEF=∠BFE=
PG(中点定义),∴EF=PF , ∴∠FEP=∠EPF , ∵∠BEP=∠EPC=90°,∴∠BEP-∠FEP=∠EPC-∠EPF , 即∠BEF=∠FPC , ∵四边形ABCD为菱形,∴AB=BC , ∠ABC=180°-∠A=70°,∵E , F分别为AB , BC的中点,∴BE=BF , ∠BEF=∠BFE= ![]() (180°-70°)=55°,∴∠FPC=55°.
(180°-70°)=55°,∴∠FPC=55°.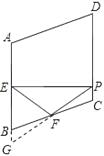
【解析】延长PF交AB的延长线于点G . 根据已知可得∠ABC , ∠BEF , ∠BFE的度数,再根据余角的性质可得到∠EPF的度数,从而不难求得∠FPC的度数.
【考点精析】关于本题考查的勾股定理的概念和菱形的性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,AE⊥BC , AF⊥CD , 且E , F分别为BC , CD的中点,求∠EAF .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图:
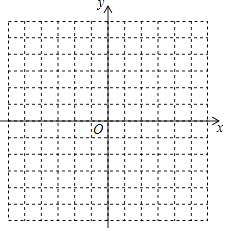
(1)在如图所示的平面直角坐标系中表示下面各点:
A(0,3);B(5,0);C(3,﹣5);D(﹣3,﹣5);E(3,5);
(2)A点到原点的距离是?
(3)将点C向x轴的负方向平移6个单位,它与哪个点重合.
(4)连接CE,则直线CE与y轴是什么位置关系?
(5)点D分别到x、y轴的距离是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线a∥b,b∥c,则直线a、c的位置关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(x﹣2)3=27,则x=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1∥l2 , 直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点

(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2x﹣k=0的一个根为﹣1,则它的另一根为 .
相关试题

