【题目】等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,以下结论:①∠APO=∠DCO; ②∠APO+∠DCO=30°;③△OPC为等边三角形;④AC=AD+AP;⑤![]() . 其中正确的有( )
. 其中正确的有( )
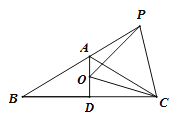
A. 2个 B. 3个 C. 4个 D. 5个
参考答案:
【答案】B
【解析】如图,
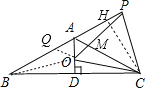
①连接OB,
∵AB=AC,BD=CD,
∴AD是BC垂直平分线,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DBO=∠DCO,
∵∠ABO+∠DBO=30°,
∴∠APO+∠DCO=30°.故①正确;
②∵△OBP中,∠BOP=180°∠OPB∠OBP,
△BOC中,∠BOC=180°∠OBC∠OCB,
∴∠POC=360°∠BOP∠BOC=∠OPB+∠OBP+∠OBC+∠OCB,
∵∠OPB=∠OBP,∠OBC=∠OCB,
∴∠POC=2∠ABD=60°,
∵PO=OC,
∴△OPC是等边三角形,故②正确;
③在AB上找到Q点使得AQ=OA,则△AOQ为等边三角形,
则∠BQO=∠PAO=120°,
在△BQO和△PAO中,
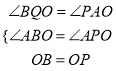
∴△BQO≌△PAO(AAS),
∴PA=BQ,
∵AB=BQ+AQ,
∴AC=AO+AP,故③正确;
④作CH⊥CD,

∵∠HCB=60,∠PCO=60,
∴∠PCH=∠OCD,
在△CDO和△CHP中,
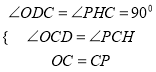
∴△CDO≌△CHP(AAS),
∴S△OCD=S△CHP
∴CH=CD,
∵CD=BD,
∴BD=CH,
在RT△ABD和RT△ACH中,
![]()
∴RT△ABD≌RT△ACH(HL),
∴S△ABD=S△AHC,
∵四边形OAPC面积=S△OAC+S△AHC+S△CHP,S△ABC=S△AOC+S△ABD+S△OCD
∴四边形OAPC面积=S△ABC.故④正确。
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,若∠B=∠C=2∠A,则∠A的度数为( )
A.72°
B.45°
C.36°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 (其中b,c为常数,c>0)的顶点恰为函数
(其中b,c为常数,c>0)的顶点恰为函数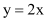 和
和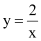 的其中一个交点.则当
的其中一个交点.则当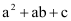 >
>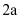 >
>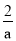 时,a的取值范围是 .
时,a的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△AOB中,∠AOB=90,AO=5,BO=3,点E、M是线段AB上的两个不同的动点(不与端点重合),分别过E、M作AO的垂线,垂足分别为K、L.
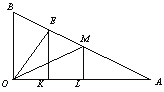
①△OEK面积S的最大值为 ;
②若以OE、OM为边构造平行四边形EOMF,当EM⊥OF时,OK+OL= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=x+b的图像经过A(2,y1),B(4,y2),则y1和y2的大小关系为( )
A.y1>y2B.y1≥y2C.y1<y2D.y1≤y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.两条不相交的直线就是平行线
B.过任意一点可以作已知直线的一条平行线
C.过直线外任意一点作已知直线的垂线,可以作无数条
D.直线外一点与直线上各点所连接的所有线段中,垂线段最短
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解一元二次方程x2-2x-3=0时,方程变形正确的是( )
A. (x-1)2=2 B. (x-1)2=4 C. (x-1)2=1 D. (x-1)2=7
相关试题

