【题目】随着电影《流浪地球》的热映,科幻大神刘慈欣的著作受到广大书迷的追捧,《流浪地球》《球状闪电》《三体》《超新星纪元》四部小说在某网上书城热销.已知《流浪地球》的销售单价与《球状闪电》相同,《三体》的销售单价是《超新星纪元》单价的3倍,《流浪地球》与《超新星纪元》的单价和大于40元且不超过50元;若自电影上映以来,《流浪地球》与《超新星纪元》的日销售量相同,《球状闪电》的日销售量为《三体》日销售量的3倍,《流浪地球》与《三体》的日销售量和为450本,且《流浪地球》的日销售量不低于《三体》的日销量的![]() 且小于230本;《流浪地球》《三体》的日销量额之和比《球状闪电》《超新星纪元》的日销售额之和多1575元.则当《流浪地球》《三体》这2部小说日销额之和最多时,《流浪地球》的单价为_____元.
且小于230本;《流浪地球》《三体》的日销量额之和比《球状闪电》《超新星纪元》的日销售额之和多1575元.则当《流浪地球》《三体》这2部小说日销额之和最多时,《流浪地球》的单价为_____元.
参考答案:
【答案】23.75.
【解析】
设出未知数,表示四部小说的单价、数量、总价,分别根据题意,列出相应的方程或不等式,确定未知数的值,或未知数的取值范围,最后根据“当《流浪地球》《三体》这2部小说日销额之和最多时”求出相应的《流浪地球》的单价即可.
解:设《流浪地球》的单价为m元/本,《超新星纪元》单价为n元/本,则《球状闪电》的单价也为m元/本,《三体》的单价为3n元/本,
设《流浪地球》的销售量为a本,《三体》的销售量为b本,则《超新星纪元》的销售量为a本,《球状闪电》的销售量为3b本,
单价、数量、总价之间的关系可用下表表示:
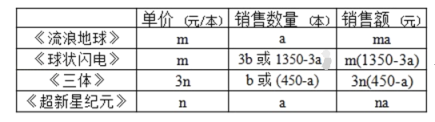
∵《流浪地球》与《三体》的日销售量和为450本,
∴a+b=450,即,b=450﹣a,
∴《流浪地球》的日销售量不低于《三体》的日销量的![]() 且小于230本,
且小于230本,
∴a≥![]() b,a<230,b=450﹣a,
b,a<230,b=450﹣a,
∴180≤a<230,
又∵《流浪地球》与《超新星纪元》的单价和大于40元且不超过50元;
∴40<m+n≤50,
∵《流浪地球》《三体》的日销量额之和比《球状闪电》《超新星纪元》的日销售额之和多1575元.
∴ma+n(1350﹣3a)=m(1350﹣3a)+na+1575,
即:(m﹣n)(4a﹣1350)=1575,
∵180≤a<230,
∴4a﹣1350<0,
∴m﹣n<0,即m<n,
当《流浪地球》《三体》这2部小说日销额之和最多时,即ma+n(1350﹣3a)=![]() [ma+n(1350﹣3a)+m(1350﹣3a)+na+1575]=
[ma+n(1350﹣3a)+m(1350﹣3a)+na+1575]= ![]() 最大
最大
即![]() 和
和![]() 最大,
最大,
∵a的最小值为180,代入(m﹣n)(4a﹣1350)=1575,得,
m﹣n=﹣![]() ,即n=m+
,即n=m+![]() ,
,
又∵40<m+n≤50,
∴m+n的最大值为50
解得:m=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点C,交AB的延长线于点E,连接CD、CE.
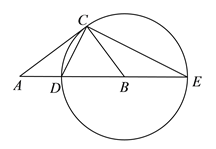
(1)求证:△ACD∽△AEC;
(2)当
 时,求tanE;
时,求tanE;(3)若AD=4,AC=4
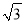 ,求△ACE的面积.
,求△ACE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与应用:
阅读1:a、b为实数,且a>0,b>0,因为
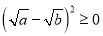 ,所以
,所以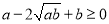 ,从而
,从而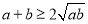 (当a=b时取等号).
(当a=b时取等号).阅读2:函数
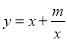 (常数m>0,x>0),由阅读1结论可知:
(常数m>0,x>0),由阅读1结论可知: 
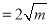 ,所以当
,所以当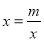 即
即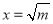 时,函数
时,函数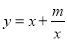 的最小值为
的最小值为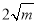 .
.阅读理解上述内容,解答下列问题:
问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为
 ,周长为
,周长为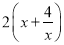 ,求当x=__________时,周长的最小值为__________.
,求当x=__________时,周长的最小值为__________.问题2:已知函数y1=x+1(x>-1)与函数y2=x2+2x+17(x>-1),当x=__________时,
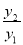 的最小值为__________.
的最小值为__________.问题3:某民办学习每天的支出总费用包含以下三个部分:一是教职工工资6400元;二是学生生活费每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的不等式组
 的所有整数解的和为5,且使关于y的分式方程
的所有整数解的和为5,且使关于y的分式方程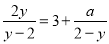 的解大于1,则满足条件的所有整数a的和是( )
的解大于1,则满足条件的所有整数a的和是( )A.16B.12C.11D.9
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,直线
 与x轴、y轴分别交于点A、C两点,点B的横坐标为2.
与x轴、y轴分别交于点A、C两点,点B的横坐标为2.
图1 图2
(1)求A、C两点的坐标和抛物线的函数关系式;
(2)点D是直线AC上方抛物线上任意一点,P为线段AC上一点,且S△PCD=2S△PAD ,求点P的坐标;
(3)如图2,另有一条直线y=-x与直线AC交于点M,N为线段OA上一点,∠AMN=∠AOM.点Q为x轴负半轴上一点,且点Q到直线MN和直线MO的距离相等,求点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9
①
乙
10
7
10
10
9
8
②
9.5
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为
 ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>0.其中正确的结论的个数是( )
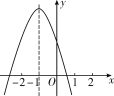
A. 1 B. 2 C. 3 D. 4
相关试题

