【题目】如图,在△ABC中,∠CAB=70°.在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )
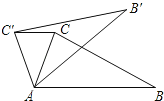
A.30° B.35° C.40° D.50°
参考答案:
【答案】C
【解析】
试题分析:旋转中心为点A,B与B′,C与C′分别是对应点,根据旋转的性质可知,旋转角∠BAB′=∠CAC′,AC=AC′,再利用平行线的性质得∠C′CA=∠CAB,把问题转化到等腰△ACC′中,根据内角和定理求∠CAC′.
解:∵CC′∥AB,∠CAB=70°,
∴∠C′CA=∠CAB=70°,
又∵C、C′为对应点,点A为旋转中心,
∴AC=AC′,即△ACC′为等腰三角形,
∴∠BAB′=∠CAC′=180°﹣2∠C′CA=40°.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB∥CD,∠C=115°,∠A=25°,则∠E=( )
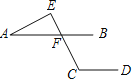
A.70° B.80° C.90° D.100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,AC⊥AB,AB=
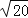 ,且AC:BD=2:3.
,且AC:BD=2:3.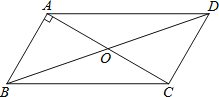
(1)求AC的长;
(2)求△AOD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x<﹣6的解集为( )
A.x<﹣3 B.x>﹣3 C.x>3 D.x<3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.
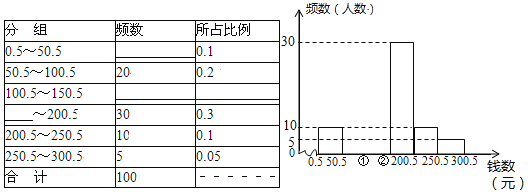
(1)补全频数分布表和直方图;
(2)研究所认为,应对消费150元以上的学生提出勤俭节约的建议,试估计应对该校4000名学生中约多少名学生提出这项建议?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方形的边长增加了2cm,面积相应增加了28cm2,则这个正方形的边长为____cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )

A. 4 B. 6 C. 8 D. 不能确定
相关试题

