【题目】如图,在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 满足
满足![]()
![]()
(1)点![]() 表示的数为 ,点
表示的数为 ,点![]() 表示的数为 .
表示的数为 .
(2)若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请在数轴上找一点
,请在数轴上找一点![]() ,使
,使![]() ,则
,则![]() 表示的数为 .
表示的数为 .
(3)如图,若在原点![]() 处放一挡板,一小球甲从点
处放一挡板,一小球甲从点![]() 处以1个单位/秒的速度向左运动;同时另一小球乙从点
处以1个单位/秒的速度向左运动;同时另一小球乙从点![]() 处以2单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为
处以2单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为![]() (秒),
(秒),
![]()
①分别表示出甲、乙两小球到原点的距离(用![]() 表示);
表示);
②求甲、乙两小球到原点的距离相等时经历的时间.
![]()
参考答案:
【答案】(1)-2、6;(2)14或![]() ;(3)①甲球与原点的距离为:
;(3)①甲球与原点的距离为:![]() ;乙到原点的距离:
;乙到原点的距离:![]() 或
或![]() ;②当
;②当![]() 秒或
秒或![]() 秒时,甲乙两小球到原点的距离相等.
秒时,甲乙两小球到原点的距离相等.
【解析】
(1)根据非负数的性质求得![]() ;
;
(2)分![]() 在线段
在线段![]() 上和线段
上和线段![]() 的延长线上两种情况讨论即可求解;
的延长线上两种情况讨论即可求解;
(3)①甲求到原点的距离=甲求运动的路程+![]() 的长,乙球到原点的距离分两种情况:当
的长,乙球到原点的距离分两种情况:当![]() 时,乙球从点
时,乙球从点![]() 处开始向左运动,一直到原点
处开始向左运动,一直到原点![]() ,此时
,此时![]() 的长度-乙球运动的路程即为乙球到原点的距离;当
的长度-乙球运动的路程即为乙球到原点的距离;当![]() 时,乙球从原点
时,乙球从原点![]() 处开始向右运动,此时乙球运动的路程-
处开始向右运动,此时乙球运动的路程-![]() 的长度即为乙球到原点的距离;
的长度即为乙球到原点的距离;
②分两种情况:当![]() 时和当
时和当![]() 时,根据甲、乙两小球到原点的距离相等列出关于
时,根据甲、乙两小球到原点的距离相等列出关于![]() 的方程,解方程即可.
的方程,解方程即可.
解:(1)∵![]() ,
,
∴![]() ,
,
解得,![]() ,
,
∴点![]() 表示的数为-2,点
表示的数为-2,点![]() 表示的数为6.
表示的数为6.
故填:-2、6;
(2)设数轴上点![]() 表示的数为
表示的数为![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
∴点![]() 不可能在
不可能在![]() 的延长线上,则
的延长线上,则![]() 点可能在线段
点可能在线段![]() 上和线段
上和线段![]() 的延长线上.
的延长线上.
①当![]() 点在线段
点在线段![]() 上时,则有
上时,则有![]() ,
,
得![]() ,解得
,解得![]() ;
;
②当![]() 点在线段
点在线段![]() 的延长线上时,则有
的延长线上时,则有![]() ,
,
得![]() ,解得
,解得![]() ;
;
故填:14或![]() ;
;
(3)①∵甲球运动的路程为:![]() ,
,![]() ,
,
∴甲球与原点的距离为:![]() ;
;
乙球到原点的距离分两种情况:
当![]() 时,乙球从点
时,乙球从点![]() 开始向左运动,一直到原点
开始向左运动,一直到原点![]() ,
,
∵![]() ,乙球运动的路程为:
,乙球运动的路程为:![]() ,
,
乙到原点的距离:![]()
当![]() 时,乙球从原点
时,乙球从原点![]() 处开始一直向右运动,
处开始一直向右运动,
此时乙球到原点的距离为:![]() ;
;
②当![]() 时,得
时,得![]() ,
,
解得![]() ;
;
当![]() 时,得
时,得![]() ,
,
解得![]() .
.
故当![]() 秒或
秒或![]() 秒时,甲乙两小球到原点的距离相等.
秒时,甲乙两小球到原点的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
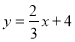 与
与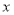 轴、
轴、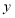 轴分别交于点
轴分别交于点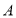 和点
和点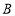 ,点
,点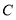 ,
,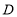 分别为线段
分别为线段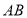 ,
,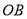 的中点,点
的中点,点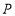 为
为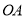 上一动点,
上一动点,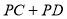 值最小时,点
值最小时,点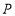 的坐标为______.
的坐标为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5cm,求AB的长.
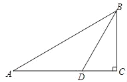
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;

2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一次函数y=mx+2的图象经过点(﹣2,6).
(1)求m的值;
(2)画出此函数的图象;
(3)平移此函数的图象,使得它与两坐标轴所围成的图形的面积为4,请直接写出此时图象所对应的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强学生的身体素质,某校长年坚持全员体育锻炼,并定期进行体能测试,下图是将某班学生的立定跳远成绩(精确到0.01米)进行整理后,画出的频数分布直方图的一部分,已知从左到右4个小组的频率分别是0.05,0.15,0.30,0.35,第5小组的频数9.
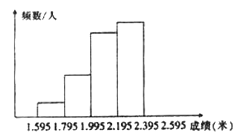
(1)请将频数分布直方图补充完整;
(2)该班参加这次测试的学生有多少人?
(3)若成绩在2.00米以上(含2.00米)的为合格,问该班成绩的合格率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】校车安全是近几年社会关注的热门话题,其中超载和超速行驶是校车事故的主要原因.小亮和同学尝试用自己所学的三角函数知识检测校车是否超速,如下图,观测点设在到白田路的距离为100米的点P处.这时,一辆校车由西向东匀速行驶,测得此校车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO =45°.
(1)求A、B之间的路程;(参考数据:
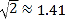 ,
, 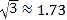 )
)(2)请判断此校车是否超过了白田路每小时60千米的限制速度?

相关试题

