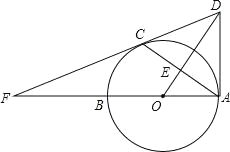
【题目】如图,已知AB是⊙O的直径,C是⊙O上的点,且OE⊥AC于点E,过点C作⊙O的切线,交OE的延长线于点D,交AB的延长线于点F,连接AD.(1)求证:AD是⊙O的切线;
(2)若cos∠BAC=![]() ,AC=8,求线段AD的长.
,AC=8,求线段AD的长.
参考答案:
【答案】(1)证明见解析(2)![]()
【解析】
试题分析:(1)连接OC,由切线的性质得出∠OCD=90°,由等腰三角形的性质得出∠COD=∠AOD,由SAS证明△COD≌△AOD,得出∠OAD=∠OCD=90°,即可得出结论;
(2)由直角三角形的锐角关系证出∠ODA=∠BAC,由垂径定理得出AE=CE=![]() AC=4,由三角函数得出
AC=4,由三角函数得出![]() ,设DE=4x,AD=5x,则AE=3x=4,求出x,即可得出结果.
,设DE=4x,AD=5x,则AE=3x=4,求出x,即可得出结果.
试题解析:(1)证明:连接OC,如图所示:
∵DC是⊙O的切线,
∴OC⊥DF,
∴∠OCD=90°,
∵OC=OA,OE⊥AC,
∴∠COD=∠AOD,
在△OAD和△OCD中,
 ,
,
∴△COD≌△AOD(SAS),
∴∠OAD=∠OCD=90°,
∴AD是⊙O的切线;
(2)解:∵∠OAD=90°,AC⊥OD,
∴∠ODA=∠BAC,AE=CE=![]() AC=4,
AC=4,
在Rt△ADE中,cos∠BAC=cos∠ADE=![]() ,
,
∴设DE=4x,AD=5x,
则AE=3x=4,
∴x=![]() ,
,
∴AD=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a+2|+(b﹣3)2=0,则a+b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠α的余角是38°15′,则∠a的补角为_____°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图1的图形称之为“8字形”.如图2,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:

(1)仔细观察,在图2中有 个以线段AC为边的“8字形”
(2)在图2中,若∠B=96°,∠C=100°,求∠P的度数.
(3)在图2中,若设∠C=α,∠B=β,∠CAP= ∠CAB,∠CDP=
∠CAB,∠CDP= ∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
(4)如图3,则∠A+∠B+∠C+∠D+∠E+∠F的度数为 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )
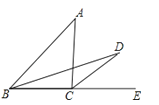
A.46°
B.92°
C.44°
D.23° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是( )

A.110°
B.100°
C.90°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,…,按此规律.则第(6)个图形中面积为1的正方形的个数为( )
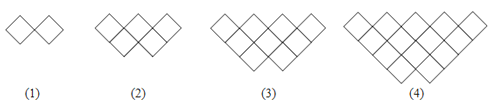
A.20
B.27
C.35
D.40
相关试题

