【题目】如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:
①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是6+4 ![]()
其中正确有 . 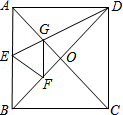
参考答案:
【答案】①④⑤
【解析】解:∵四边形ABCD是正方形,
∴∠GAD=∠ADO=45°,
由折叠的性质可得:∠ADG= ![]() ∠ADO=22.5°,故①正确.
∠ADO=22.5°,故①正确.
∵由折叠的性质可得:AE=EF,∠EFD=∠EAD=90°,
∴AE=EF<BE,
∴AE< ![]() AB,
AB,
∴ ![]() >2,
>2,
在Rt△ADE中,tan∠AED= ![]() >2,故②错误.
>2,故②错误.
∵∠AOB=90°,
∴AG=FG>OG,△AGD与△OGD同高,
∴S△AGD>S△OGD , 故③错误.
∵∠EFD=∠AOF=90°,
∴EF∥AC,
∴∠FEG=∠AGE,
∵∠AGE=∠FGE,
∴∠FEG=∠FGE,
∴EF=GF,
∵AE=EF,
∴AE=GF,
∵AE=EF=GF,AG=GF,
∴AE=EF=GF=AG,
∴四边形AEFG是菱形,故④正确.
∴∠OGF=∠OAB=45°,
∴EF=GF= ![]() OG,
OG,
∴BE= ![]() EF=
EF= ![]() ×
× ![]() OG=2OG.故⑤正确.
OG=2OG.故⑤正确.
∵四边形AEFG是菱形,
∴AB∥GF,AB=GF.
∵∠BAO=45°,∠GOF=90°,
∴△OGF时等腰直角三角形.
∵S△OGF=1,
∴ ![]() OG2=1,解得OG=
OG2=1,解得OG= ![]() ,
,
∴BE=2OG=2 ![]() ,GF=
,GF= ![]() ═2,
═2,
∴AE=GF=2,
∴AB=BE+AE=2 ![]() +2,
+2,
∴S正方形ABCD=AB2=(2 ![]() +2)2=12+8
+2)2=12+8 ![]() ,故⑥错误.
,故⑥错误.
∴其中正确结论的序号是:①④⑤共三个.
所以答案是①④⑤.
【考点精析】利用平行线的性质和等腰三角形的性质对题目进行判断即可得到答案,需要熟知两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )
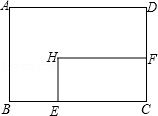
A.
B.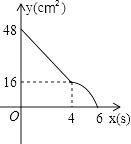
C.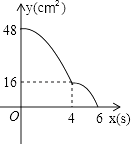
D.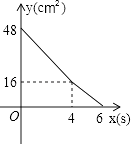
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列分式方程:
(1)
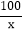 =
=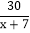 ; (2)
; (2)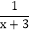 -
-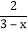 =
=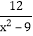
-
科目: 来源: 题型:
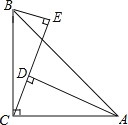
查看答案和解析>>【题目】如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)求证:△ACD≌△CBE;
(2)若AD=12,DE=7,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.

(1)求证:CF∥AB.
(2)求∠DFC的度数.
-
科目: 来源: 题型:
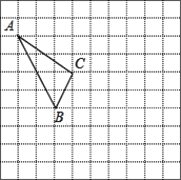
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为A(-4,5),C(-1,3).
(1)请在如图所示的网格内作出x轴、y轴;
(2)请作出△ABC关于y轴对称的△A1B1C1;
(3)写出点B1的坐标并求出△A1B1C1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,证明:AB=FA+BD;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请画出图形并直接写出正确结论.

相关试题

