【题目】已知:如图1,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).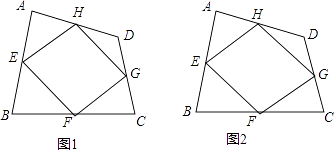
(1)四边形EFGH的形状是 , 证明你的结论.
(2)如图2,请连接四边形ABCD的对角线AC与BD,当AC与BD满足条件时,四边形EFGH是矩形;证明你的结论.
(3)你学过的哪种特殊四边形的中点四边形是矩形?说明理由.
参考答案:
【答案】
(1)平行四边形
(2)互相垂直
(3)
解:菱形的中点四边形是矩形.理由如下:
如图3,连结AC、BD.
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,FG∥BD,EH= ![]() BD,FG=
BD,FG= ![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,
∵EH∥BD,HG∥AC,
∴EH⊥HG,
∴平行四边形EFGH是矩形.
故答案为:平行四边形;互相垂直.
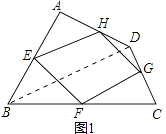
【解析】解:(1)四边形EFGH的形状是平行四边形.理由如下:
如图1,连结BD.
∵E、H分别是AB、AD中点,
∴EH∥BD,EH= ![]() BD,
BD,
同理FG∥BD,FG= ![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
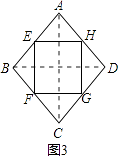
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.理由如下:
如图2,连结AC、BD.
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;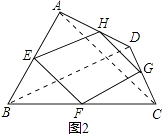
【考点精析】本题主要考查了矩形的判定方法的相关知识点,需要掌握有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若□×3xy=3x2y,则□内应填的单项式是( )
A.xy
B.3xy
C.x
D.3x -
科目: 来源: 题型:
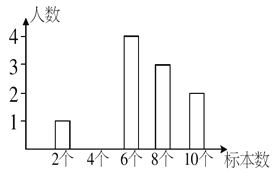
查看答案和解析>>【题目】某生物课外活动小组的同学举行植物标本制作比赛,结果统计如下:

根据表中提供的信息,回答下列问题:
(1)该组共有学生多少人?
(2)每人制作标本数在6个及以上的人数在全组人数中所占比例?
(3)平均每人制作多少个标本?
(4)补全下图的条形统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD且AE=AB.
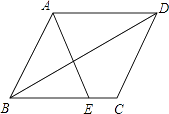
(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形. -
科目: 来源: 题型:
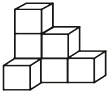
查看答案和解析>>【题目】如图是由几个相同的边长为1的小立方块搭成的几何体.
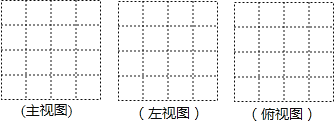
(1)请画出这个几何体的三视图;
(2)根据三视图,这个几何体的表面积为 个平方单位(包括底面积);
(3)若上述小立方块搭成的几何体的俯视图不变,各位置的小立方块个数可以改变(总数目不变),则搭成的几何体的表面积最大为 个平方单位(包括底面积) .
-
科目: 来源: 题型:
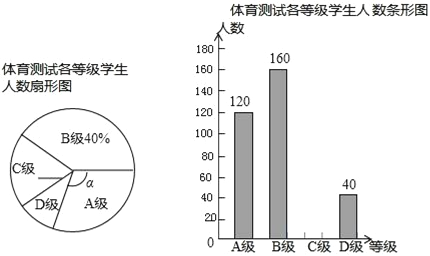
查看答案和解析>>【题目】为了解学生体育训练的情况,某市从全市九年级学生中随机抽取部分学生进行了一次体育科目测试(把成绩结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)求本次抽样测试的学生人数;
(2)求扇形图中∠α的度数,并把条形统计图补充完整;
(3)该市九年级共有学生9000名,如果全部参加这次体育测试,则测试等级为D的约有多少人?
-
科目: 来源: 题型:
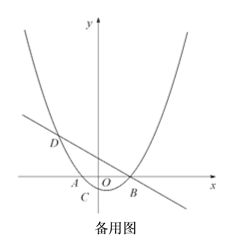
查看答案和解析>>【题目】如图,已知抛物线
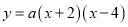 (a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线
(a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线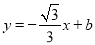 与抛物线的另一交点为D,且点D的横坐标为﹣5.
与抛物线的另一交点为D,且点D的横坐标为﹣5.(1)求抛物线的函数表达式;
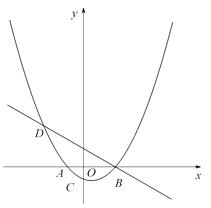
(2)P为直线BD下方的抛物线上的一点,连接PD、PB, 求△PBD面积的最大值.
(3)设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
相关试题

