搜索
【题目】如图，在四边形ABCD中，AD∥BC，∠C＝90°，AD＝21cm，BC＝16cm，DC＝12cm，动点P从D开始沿DA向A以2cm/s的速度运动；动点Q从点C开始向B以1cm/s的速度运动.P、Q分别从点D、C同时出发，当其中一点到达端点时，另外一点也随之停止运动，设运动时间为ts.
（1）如图1，当t为何值时，四边形APQB是平行四边形
（2）△BPQ是等腰三角形，则有三种情况：BP＝BQ，PB＝PQ，QP＝QB.
①当BP＝BQ时，此情况不成立；
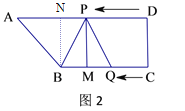
②当PB＝PQ时，如图2，作PM⊥BC，则BM＝_________________，QM＝_________________，（用含t的式子表示），得到t＝________________.
③当QP＝QB时，请求出t的值.
参考答案：
【答案】（1）5；（2）②16－2t，t，
；③3.5
【解析】【试题分析】（1）当AP=QB时，四边形APQB是平行四边形；
(2)根据图形，列出表达式即可.
【试题解析】
（1）由题意得：21-2t=16-t，解得：t=5.
（2）②作BN垂直AD，垂足为N.
BM＝QN=16-2t，QM＝PD-CQ=2t-t=t，当PB=PQ时，得到BM=QM，即16-2t =t,解得：t＝.
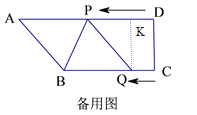
③作QK垂直AD，垂足为K.
QB=16-t,
根据QP＝QB，得：
解得：t=3.5.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂计划生产A，B两种产品共10件，其生产成本和利润如下表：
A种产品
B种产品
成本（万元/件）
2
5
利润（万元/件）
1
3
（1）若工厂计划获利14万元，问A，B两种产品应分别生产多少件？
（2）若工厂计划投入资金不多于44万元，且获利多于14万元，问工厂有哪几种生产方案？
（3）在（2）的条件下，哪种生产方案获利最大？并求出最大利润．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有两个
与
，保持不动，且的一边
，另一边DE与直线OB相交于点F．
若
，
，解答下列问题：
如图，当点E、O、D在同一条直线上，即点O与点F重合，则
______；
当点E、O、D不在同一条直线上，画出图形并求
的度数；
在
的前提下，若
，
，且
，请直接写出的度数
用含
、
的式子表示
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角坐标系中，已知点
，
，
，a是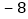
的立方根，方程
是关于x，y的二元一次方程，d为不等式组
的最大整数解．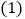
求点A、B、C的坐标；
如图1，若D为y轴负半轴上的一个动点，当
时，
与
的平分线交于M点，求
的度数；
如图2，若D为y轴负半轴上的一个动点，连BD交x轴于点E，问是否存在点D，使
？若存在，请求出D的纵坐标
的取值范围；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在⊿
中，
,点
分别在
边上，且
, 
.⑴.求证：⊿
是等腰三角形；⑵.当
时，求
的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了了解同学们每月零花钱的数额，校园小记者随机调查了本校部分同学，根据调查结果，绘制出了如下两个尚不完整的统计图表．
调查结果统计表
组别
分组（单位：元）
人数
A
0≤x＜30
4
B
30≤x＜60
16
C
60≤x＜90
a
D
90≤x＜120
b
E
x≥120
2
请根据以上图表，解答下列问题：
（1）填空：这次被调查的同学共有__人，a+b=__，m=___；
（2）求扇形统计图中扇形C的圆心角度数；
（3）该校共有学生1000人，请估计每月零花钱的数额x在60≤x＜120范围的人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直角坐标系中，
的顶点都在网格点上，其中，C点坐标为
．
填空：点A的坐标是______，点B的坐标是______；
将先向左平移2个单位长度，再向上平移1个单位长度，得到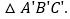
请写出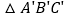
的三个顶点坐标；
求的面积．
相关试题
