【题目】如图,已知直线l及其两侧两点A、B.

(1)在直线l上求一点O,使到A、B两点距离之和最短;
(2)在直线l上求一点P,使PA=PB;
(3)在直线l上求一点Q,使l平分∠AQB.
参考答案:
【答案】见解析
【解析】
试题分析:(1)根据两点之间线段最短,连接AB,线段AB交直线l于点O,则O为所求点;
(2)根据线段垂直平分线的性质连接AB,在作出线段AB的垂直平分线即可;
(3)作B关于直线l的对称点B′,连接AB′交直线l与点Q,连接BQ,由三角形全等的判定定理求出△BDQ≌△B′DQ,再由全等三角形的性质可得出∠BQD=∠B′QD,即直线l平分∠AQB.
解:(1)连接AB,线段AB交直线l于点O,
∵点A、O、B在一条直线上,
∴O点即为所求点;

(2)连接AB,
分别以A、B两点为圆心,以任意长为半径作圆,两圆相交于C、D两点,连接CD与直线l相交于P点,
连接BD、AD、BP、AP、BC、AC,
∵BD=AD=BC=AC,
∴△BCD≌△ACD,
∴∠BED=∠AED=90°,
∴CD是线段AB的垂直平分线,
∵P是CD上的点,
∴PA=PB;
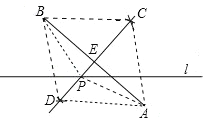
(3)作B关于直线l的对称点B′,连接AB′交直线l与点Q,连接BQ,
∵B与B′两点关于直线l对称,
∴BD=B′D,DQ=DQ,∠BDQ=∠B′DQ,
∴△BDQ≌△B′DQ,
∴∠BQD=∠B′QD,即直线l平分∠AQB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题6分)如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负。如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
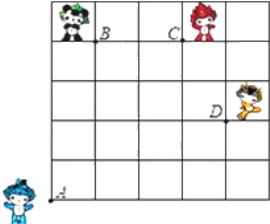
(1)A→C( , );B→C( , );C→ (-3,-4);
(2)若贝贝的行走路线为A→B→C→D,请计算贝贝走过的路程;
(3)若贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-2,-2),请在图中标出妮妮的位置E点.
(4)在(3)中贝贝若每走1m需消耗1.5焦耳的能量,则贝贝寻找妮妮过程中共需消耗多少焦耳的能量?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到△A1OB1,若点B的坐标为(2,1),则点B的对应点B1的坐标为( )
A.(1,2) B.(2,﹣1) C.(﹣2,1) D.(﹣2,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(﹣2,3)关于y轴对称的点A′的坐标是( )
A.(-2,6) B.(2,3) C.(-2,-3) D.(2,-3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
 (2) 12+(-8)+11+(-2)+(-12)
(2) 12+(-8)+11+(-2)+(-12) +
+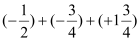 (4) (-24)÷2×(-3)÷(-6)
(4) (-24)÷2×(-3)÷(-6) (5)
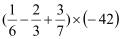 (6)(-4)×(-2
(6)(-4)×(-2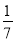 )+(-8)×(-2
)+(-8)×(-2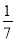 )+12×(-2
)+12×(-2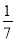 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】
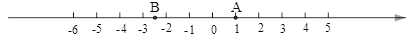
⑴请你根据图中A、B两点的位置,分别写出它们所表示的有理数A: B: ;
⑵观察数轴,与点A的距离为4的点表示的数是: ;
⑶若将数轴折叠,使得A点与-3表示的点重合,则B点与数 表示的点重合
⑷若数轴上M、N两点之间的距离为2016(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M: N:
相关试题

