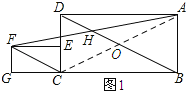
【题目】如图,已知在矩形ABCD中,BC=2CD=2a,点E在边CD上,在矩形ABCD的左侧作矩形ECGF,使CG=2GF=2b,连接BD,CF,连结AF交BD于点H.

(1)求证:BD∥CF;
(2)求证:H是AF的中点;
(3)连结CH,若HC⊥BD,求a:b的值.
参考答案:
【答案】(1)见解析;(2)见解析;(3)a:b=![]() .
.
【解析】
试题分析:(1)由矩形的性质可知∠G=∠DCB=90°,由BC=2CD=2a,CG=2GF=2b,可知![]() ,依据两边对应成比例且夹角相等的两个三角形相似可知:△FGC∽△DCB,由相似三角形的性质可知∠FCG=∠DBC,由平行线的判定定理可知:BD∥CF;
,依据两边对应成比例且夹角相等的两个三角形相似可知:△FGC∽△DCB,由相似三角形的性质可知∠FCG=∠DBC,由平行线的判定定理可知:BD∥CF;
(2)如图1所示:连接AC,交BD于点O.由矩形的性质可知:OC=OA,由平行线分线段成比例定理可知HF=AH;
(3)如图2所示:连接CH,CA,AC与BD交于点O.由勾股定理可知:FC=![]() b,AC=
b,AC=![]() a,由矩形的对角线的性质可知DB=AC=
a,由矩形的对角线的性质可知DB=AC=![]() a,CO=
a,CO=![]() AC=
AC=![]() .由(2)可知HO是△AFC的中位线,由三角形中位线的性质可知:HO=
.由(2)可知HO是△AFC的中位线,由三角形中位线的性质可知:HO=![]() .在△BCD中,利用面积法可求得CH=
.在△BCD中,利用面积法可求得CH=![]() ,最后在△COH中,由勾股定理得到:(
,最后在△COH中,由勾股定理得到:(![]() )2+(
)2+(![]() )2=(
)2=(![]() a)2,从而可求得a:b=
a)2,从而可求得a:b=![]() .
.
解:(1)∵四边形ABCD、四边形ECGF均为矩形,
∴∠G=∠DCB=90°.
∵BC=2CD=2a,CG=2GF=2b,
∴![]() .
.
∴△FGC∽△DCB.
∴∠FCG=∠DBC.
∴BD∥CF.
(2)如图1所示:连接AC,交BD于点O.
∵四边形ABCD为矩形,
∴OC=OA.
又∵FC∥BD,
∴HF=AH.
∴点H是AF的中点.
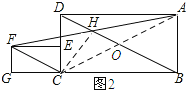
(3)如图2所示:连接CH,CA,AC与BD交于点O.
由勾股定理可知:FC=![]() =
=![]() b,AC=
b,AC=![]() =
=![]() a.
a.
∵四边形ABCD为矩形,
∴DB=AC=![]() a,CO=
a,CO=![]() AC=
AC=![]() .
.
∵HO是△AFC的中位线,
∴HO=![]() FC=
FC=![]() .
.
∵![]() ,
,
∴CH=![]() =
=![]() .
.
在△COH中,由勾股定理可知:HO2+CH2=OC2,即(![]() )2+(
)2+(![]() )2=(
)2=(![]() a)2.
a)2.
整理得:a2=![]() .
.
∴a:b=![]() .
.
-
科目: 来源: 题型:
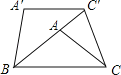
查看答案和解析>>【题目】如图,将△ABC绕点B逆时针旋转40°,得到△A′B′C′,若点C′恰好落在边BA的延长线上,且A′C′∥BC,连接CC′,则∠ACC′= 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,双曲线y=
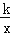 经过点A(1,2),过点A作y轴的垂线,垂足为B,交双曲线y=﹣
经过点A(1,2),过点A作y轴的垂线,垂足为B,交双曲线y=﹣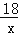 于点C,直线y=m(m≠0)分别交双曲线y=﹣
于点C,直线y=m(m≠0)分别交双曲线y=﹣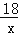 、y=
、y=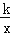 于点P、Q.
于点P、Q.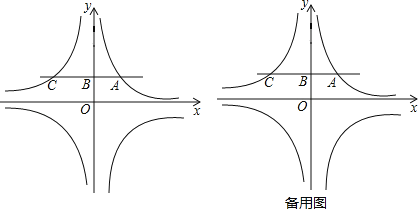
(1)求k的值;
(2)若△OAP为直角三角形,求点P的坐标;
(3)△OCQ的面积记为S△OCQ,△OAP的面积记为S△OAP,试比较S△OCQ与S△OAP的大小(直接写出结论).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市一天的最高气温为2℃,最低气温为﹣8℃,那么这天的最高气温比最低气温高( ).
A.﹣10℃ B.﹣6℃ C.10℃ D.6℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】将点A(2,1)向上平移3个单位得到点B,则点B的坐标是( )
A. (5,1) B. (-1,4)
C. (5,4) D. (2,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次体育达标测试中,小明所在小组的六位同学的立定跳远成绩如下(单位:m):2.00,2.11,2.21,2.15,2.20,2.17,那么这组数据的中位数是( ).
A.2.16 B.2.15 C.2.14 D.2.13
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一列不全为零的数除了第一个数和最后一个数外,每个数都等于前后与它相邻的两数之和,则称这列数具有“波动性质”.已知一列数共有2016个,且具有“波动性质”,则这2016个数的和为( )
A.﹣64 B.0 C.18 D.64
相关试题

