【题目】如图,函数y= ![]() 的图象过点A(1,2).
的图象过点A(1,2). 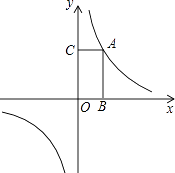
(1)求该函数的解析式;
(2)过点A分别向x轴和y轴作垂线,垂足为B和C,求四边形ABOC的面积;
(3)求证:过此函数图象上任意一点分别向x轴和y轴作垂线,这两条垂线与两坐标轴所围成矩形的面积为定值.
参考答案:
【答案】
(1)解:∵函数y= ![]() 的图象过点A(1,2),
的图象过点A(1,2),
∴将点A的坐标代入反比例函数解析式,
得2= ![]() ,解得:k=2,
,解得:k=2,
∴反比例函数的解析式为y= ![]()
(2)解:∵点A是反比例函数上一点,
∴矩形ABOC的面积S=ACAB=|xy|=|k|=2
(3)解:设图象上任一点的坐标(x,y),
∴过这点分别向x轴和y轴作垂线,矩形面积为|xy|=|k|=2,
∴矩形的面积为定值.
【解析】(1)将点A的坐标代入反比例函数解析式,即可求出k值;(2)由于点A是反比例函数上一点,矩形ABOC的面积S=|k|.(3)设图象上任一点的坐标(x,y),根据矩形的面积公式,可得出结论.
【考点精析】本题主要考查了比例系数k的几何意义的相关知识点,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按下面的程序计算:

若开始输入的x值为正整数,最后输出的结果为556,则开始输入的x值为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=mx+n与
 ,其中m≠0,n≠0,那么它们在同一坐标系中的图象可能是( )
,其中m≠0,n≠0,那么它们在同一坐标系中的图象可能是( )A.
 B.
B. C.
C.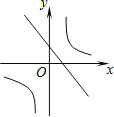 D.
D.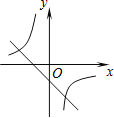
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y=
 (x>0)和y=-
(x>0)和y=- (x>0)的图象于A,B两点,C是y轴上任意一点,则△ABC的面积为________.
(x>0)的图象于A,B两点,C是y轴上任意一点,则△ABC的面积为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC的角平分线AD交BC于E,交△ABC的外接圆⊙O于D.

(1)求证:△ABE∽△ADC;
(2)请连接BD,OB,OC,OD,且OD交BC于点F,若点F恰好是OD的中点.求证:四边形OBDC是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.

(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y1=x(x≥0),y2=
 (x>0)的图象如图所示,则以下结论:
(x>0)的图象如图所示,则以下结论:①两函数图象的交点A的坐标为(2,2);②当x>2时,y1>y2;
③BC=2;④两函数图象构成的图形是轴对称图形;
⑤当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.
其中正确结论的序号是____________.

相关试题

