【题目】在平面直角坐标系中,A(0,a)、B(﹣b,0),若b=![]() +4,C点是B点关于y轴的对称点.
+4,C点是B点关于y轴的对称点.
(1)判断△ABC的形状并证明;
(2)P点在第一象限,且∠APC=135°,试探究关于PA、PB、PC三条线段的确定数量关系;
(3)E点在BC上,F为线段AE的中点,EF绕E点顺时针旋转60°得到EG,E点从B点沿BC运动到C点,求G点随E点运动的路径长.
参考答案:
【答案】(1)△ABC是等腰直角三角形,理由详见解析;(2)当点P在△AOC的外部时,PB﹣PC=![]() PA,当点P在△AOC内部时,PA2=2PB2+PC2,证明详见解析;(3)6
PA,当点P在△AOC内部时,PA2=2PB2+PC2,证明详见解析;(3)6![]() .
.
【解析】
(1)如图1中,△ABC是等腰直角三角形.根据等腰直角三角形的定义即可判断.
(2)结论::①当点P在△AOC的外部时,PB﹣PC=![]() PA.如图2中,作AE⊥PA交PB于E.证明△BAE≌△CAP(SAS),△AEP是等腰直角三角形即可.②当点P在△AOC内部时,如图2﹣1中,PA2=2PB2+PC2.
PA.如图2中,作AE⊥PA交PB于E.证明△BAE≌△CAP(SAS),△AEP是等腰直角三角形即可.②当点P在△AOC内部时,如图2﹣1中,PA2=2PB2+PC2.
(3)如图3中,连接AG,OG.首先证明∠EOG=30°,推出点G的运动轨迹是线段(图中线段G″G′),利用等腰直角三角形的性质求出G′G″即可.
(1)如图1中,△ABC是等腰直角三角形.理由如下:

∵b=![]()
∴a﹣4≥0,8﹣2a≥0
∴a=4,b=4
∴A(0,4),B(0,﹣4)
∵B,C关于y轴对称,
∴C(4,0),
∴OA=OB=OC,
∵∠AOB=∠AOC=90°,
∴∠ABC=∠ACB=45°,
∴AB=AC,∠BAC=90°,
∴△ABC是等腰直角三角形.
(2)结论:①当点P在△AOC的外部时,PB﹣PC=![]() PA.
PA.
理由:如图2中,作AE⊥PA交PB于E.
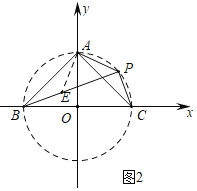
∵∠APC+∠ABC=180°,
∴A,B,C,P四点共圆,
∴∠APE=∠ACB=45°,
∵∠EAP=90°,
∴∠AEP=∠APE=45°,
∴AE=AP,
∵∠BAC=∠EAP=90°,
∴∠BAE=∠CAP,
∵AB=AC,AE=AP,
∴△BAE≌△CAP(SAS),
∴BE=PC,
∴PB﹣PC=PB﹣BE=PE=![]() PA.
PA.
②当点P在△AOC内部时,如图2﹣1中,PA2=2PB2+PC2.
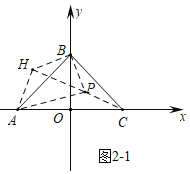
理由:将△PBC绕点B顺时针旋转90°得到△HBA,
∵∠BHP=45°,∠BHA=∠BPC=135°,
∴∠AHP=90°,
∴PA2=AH2+PH2,
∵PC=AH,PH=![]() PB,
PB,
∴PA2=PC2+2PB2.
(3)如图3中,连接AG,OG.

∵EF=EG,∠FEG=60°,
∴△EFG是等边三角形,
∴FG=FE=FA,
∴∠AGE=90°,∠EAG=30°,
∵∠AGE=∠AOE=90°,
∴A,E,G,O四点共圆,
∴∠EOG=∠EAG=30°,
∴点G的运动轨迹是线段(图中线段G″G′),
由题意△G′AG″是等腰直角三角形,AG′=AG″=2![]() ,
,
∴G′G″=6![]() .
.
∴当E点从B点沿BC运动到C点,G点随E点运动的路径长为6![]() .
.
-
科目: 来源: 题型:
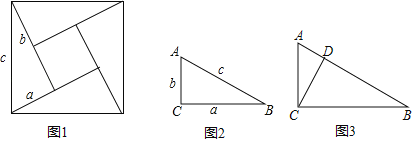
查看答案和解析>>【题目】如图1所示,有四个同样大小的直角三角形,两条直角边分别为a、b,斜边为c,拼成一个正方形,中间留有一个小正方形.
(1)利用它们之间的面积关系,探索出关于a、b、c的等式;
(2)利用(1)中发现的直角三角形中两直角边a,b和斜边c之间的关系,完成问题:如图2,在直角△ABC中,∠C=90°,且c=6,a+b=8,则△ABC的面积为 ;
(3)如图3所示,CD是直角△ABC中斜边上的高,试证明CD2=ADBD.
-
科目: 来源: 题型:
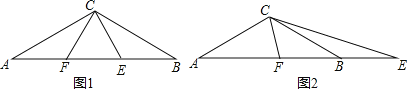
查看答案和解析>>【题目】如图1,△ABC中,CA=CB,∠ACB=120°,AB=3,点E、F在直线AB上,且∠ECF=60°.
(1)求AC边的长;
(2)如图1,点E、F在线段AB上时,若EF=AF,求证:BE=EF;
(3)如图2,F在AB上,E在AB的延长线上时,AF=m,BE=n,则n= (用含m的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
①当x>0时,y1>y2; ②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在; ④使得M=1的x值是
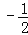 或
或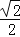 .
.其中正确的是( )

A.①② B.①④ C.②③ D.③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一组数据a1,a2,a3的平均数为4,方差为3,那么数据a1+2,a2+2,a3+2的平均数和方差分别是( )
A. 4,3B. 6,3C. 3,4D. 6,5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知点A、B是反比例函数y=﹣
 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
【答案】

【解析】过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,如图所示.

∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵AD⊥y轴,BE⊥y轴,
∴∠ACD+∠CAD=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,∠BCE=∠CAD.
在△ACD和△CBE中,由
 ,
,∴△ACD≌△CBE(ASA).
设点B的坐标为(m,﹣
 )(m<0),则E(0,﹣
)(m<0),则E(0,﹣ ),点D(0,3﹣m),点A(﹣
),点D(0,3﹣m),点A(﹣ ﹣3,3﹣m),
﹣3,3﹣m),∵点A(﹣
 ﹣3,3﹣m)在反比例函数y=﹣
﹣3,3﹣m)在反比例函数y=﹣ 上,
上, ,解得:m=﹣3,m=2(舍去).
,解得:m=﹣3,m=2(舍去).∴点A的坐标为(﹣1,6),点B的坐标为(﹣3,2),点F的坐标为(﹣1,2),
∴BF=2,AF=4,

故答案为:2
 .
.【点睛】
过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,根据角的计算得出“∠ACD=∠CBE,∠BCE=∠CAD”,由此证出△ACD≌△CBE;再设点B的坐标为(m,﹣
 ),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.【题型】填空题
【结束】
18【题目】二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y=
 x-3与x轴,y轴分别交于点A和点B.
x-3与x轴,y轴分别交于点A和点B.(1)求点A和点B的坐标;
(2)将直线l1向上平移6个单位后得到直线l2,求直线l2的函数解析式;
(3)设直线l2与x轴的交点为M,则△MAB的面积是______.
相关试题

