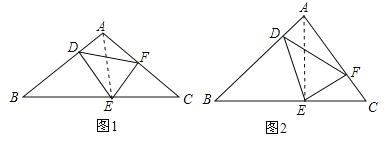
【题目】在△ABC中,点D,E,F分别在AB,BC,AC上,且∠ADF+∠DEC=180°,∠AFE=∠BDE.
(1)如图1,当DE=DF时,图1中是否存在与AB相等的线段?若存在,请找出,并加以证明;若不存在,说明理由;
(2)如图2,当DE=kDF(其中0<k<1)时,若∠A=90°,AF=m,求BD的长(用含k,m的式子表示).

参考答案:
【答案】(1)AB=BE;(2)BD=![]() .
.
【解析】
试题分析:(1)如图1,连结AE.由DE=DF,得到∠DEF=∠DFE,由∠ADF+∠DEC=180°,得到∠ADF=∠DEB.由∠AFE=∠BDE,得到∠AFE+∠ADE=180°,得到A、D、E、F四点共圆,由圆周角定理得出∠DAE=∠DFE=∠DEF,∠ADF=∠AEF.再由∠ADF=∠DEB=∠AEF,得出∠AEF+∠AED=∠DEB+∠AED,则∠AEB=∠DEF=∠BAE,由等角对等边得出AB=BE;
(2)如图2,连结AE.由A、D、E、F四点共圆,得到∠ADF=∠AEF,由∠DAF=90°,得到∠DEF=90°,再证明∠DEB=∠AEF.又∠AFE=∠BDE,得到△BDE∽△AFE,利用相似三角形对应边成比例得到![]() .在Rt△DEF中,利用勾股定理求出EF=
.在Rt△DEF中,利用勾股定理求出EF=![]() DF,然后将AF=m,DE=kDF代入,计算即可求解.
DF,然后将AF=m,DE=kDF代入,计算即可求解.
试题解析:(1)如图1,连结AE.∵DE=DF,∴∠DEF=∠DFE,∵∠ADF+∠DEC=180°,∴∠ADF=∠DEB,∵∠AFE=∠BDE,∴∠AFE+∠ADE=180°,∴A、D、E、F四点共圆,∴∠DAE=∠DFE=∠DEF,∠ADF=∠AEF,∵∠ADF=∠DEB=∠AEF,∴∠AEF+∠AED=∠DEB+∠AED,∴∠AEB=∠DEF=∠BAE,∴AB=BE;
(2)如图2,连结AE.∵∠AFE=∠BDE,∴∠AFE+∠ADE=180°,∴A、D、E、F四点共圆,∴∠ADF=∠AEF,∵∠DAF=90°,∴∠DEF=90°,∵∠ADF+∠DEC=180°,∴∠ADF=∠DEB,∵∠ADF=∠AEF,∴∠DEB=∠AEF,在△BDE与△AFE中,∵∠DEB=∠AEF,∠BDE=∠AFE,∴△BDE∽△AFE,∴![]() ,在直角△DEF中,∵∠DEF=90°,DE=kDF,∴EF=
,在直角△DEF中,∵∠DEF=90°,DE=kDF,∴EF=![]() =
=![]() DF,∴
DF,∴![]() =
=![]() ,∴BD=
,∴BD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点A(0,0),B(2,﹣2),C(4,0),D(2,2),则以这四个点为顶点的四边形ABCD是( )
A. 正方形 B. 菱形 C. 梯形 D. 矩形
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(2a2)3的结果是( )
A. 2a5 B. 2a6 C. 6a6 D. 8a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数的绝对值越小,则该数在数轴上所对应的点,离原点越。
-
科目: 来源: 题型:
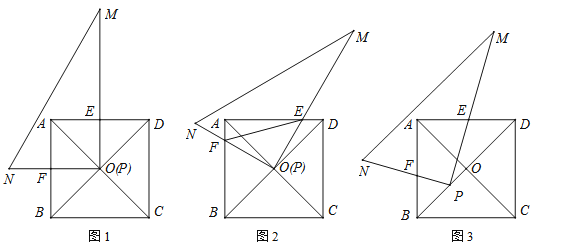
查看答案和解析>>【题目】在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.
(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;
(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).
①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;
②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;
③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD=mBP时,请直接写出PE与PF的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校把学生的笔试成绩、实践能力和成长记录三项成绩分别按50%、20%和30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩(单位:分)记录如下,学期总评成绩优秀的学生是__________.
笔试成绩
实践能力
成长记录
甲
90
83
95
乙
88
90
95
丙
90
88
90
-
科目: 来源: 题型:
查看答案和解析>>【题目】一水库里有鲤鱼、鲫鱼、草鱼共2 000尾,小明通过多次捕捞试验,发现鲤鱼、草鱼的概率是51%和26%,则水库里有_____尾鲫鱼.
相关试题

