【题目】解不等式组  ,并把它的解集在数轴上表示出来.再求它的所有的非负整数解.
,并把它的解集在数轴上表示出来.再求它的所有的非负整数解.
参考答案:
【答案】解:  ,由①得,x>﹣2,由②得,x≤
,由①得,x>﹣2,由②得,x≤ ![]() ,
,
故此不等式组的解集为:﹣2<x≤ ![]() ,
,
在数轴上表示为:
 ,
,
它的所有的非负整数解为:0,1,2.
【解析】分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来,写出符合条件的x的非负整数解即可.
【考点精析】根据题目的已知条件,利用不等式的解集在数轴上的表示和一元一次不等式组的解法的相关知识可以得到问题的答案,需要掌握不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种禽流感病毒的直径为0.000000012米,将这个数用科学记数法表示为_________ 米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用同样规格的黑白两色的正方形瓷砖铺设矩形地面,请观察下列图形并解答有关问题.
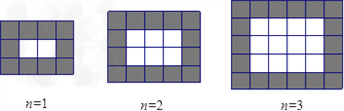
(1)在第n个图中,第一横行共_________ 块瓷砖,第一竖列共有_________ 块瓷砖;(均用含n的代数式表示)
(2)设铺设地面所用瓷砖的总块数为y,请写出y与(1)中的n的函数关系式;
(3)按上述铺设方案,铺一块这样的矩形地面共用了506块瓷砖,求此时n的值;
(4)黑瓷砖每块4元,白瓷砖每块3元,问题(3)中,共花多少元购买瓷砖;
(5)是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,2017)与点A′(﹣2018,b)是关于原点O的对称点,则a+b的值为( )
A. 1 B. 5 C. 6 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.3a+2a=5a2
B.3a+3b=3ab
C.2a2bc﹣a2bc=a2bc
D.a5﹣a2=a3 -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一边长是8cm,另一边长是3cm,则它的周长是______ .
相关试题

