【题目】已知α、β是方程x2+x﹣6=0的两根,则α2β+αβ=_____.
参考答案:
【答案】12或﹣18.
【解析】
先利用根与系数的关系得到α+β=﹣1,αβ=﹣6,所以α2β+αβ=αβ(α+1)=﹣6(α+1),再解方程解方程x2+x﹣6=0得x1=﹣3,x2=2,然后把α=﹣3和α=2分别代入计算即可.
根据题意得α+β=﹣1,αβ=﹣6,
所以α2β+αβ=αβ(α+1)=﹣6(α+1),
而解方程x2+x﹣6=0得x1=﹣3,x2=2,
当α=﹣3时,原式=﹣6(﹣3+1)=12;
当α=2时,原式=﹣6(2+1)=﹣18.
故答案为12或﹣18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据报道,全省将有近15万人参加2018年省公务员录用考试笔试,数字15万用科学记数法表示为:_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个能够完全重合的图形称为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算: ①33°52′+21°54′=;
②18.18°=°′″. -
科目: 来源: 题型:
查看答案和解析>>【题目】不能用尺规作图作出唯一三角形的是( )
A.已知两角和夹边
B.已知两边和夹角
C.已知两角和其中一角的对边
D.已知两边和其中一边的对角 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a3a4=a12
B.3a22a3=6a6
C.(﹣2x2y)3=﹣8x6y3
D.(﹣3a2b3)2=6a4b6 -
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(1)若直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数y=
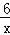 的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;(3)当常数k满足
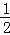 ≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
相关试题

